3. Getting started with prenspire

import random
from pathlib import Path

import lmfit
import numpy as np

from clophfit import prenspire
from clophfit.fitting.core import (
    DataArray,
    Dataset,
    analyze_spectra,
    analyze_spectra_glob,
    fit_binding_glob,
    weight_multi_ds_titration,
)
from clophfit.fitting.plotting import plot_emcee

%load_ext autoreload
%autoreload 2
tpath = Path("../../tests/EnSpire")

ef1 = prenspire.EnspireFile(tpath / "h148g-spettroC.csv")
ef2 = prenspire.EnspireFile(tpath / "e2-T-without_sample_column.csv")
ef3 = prenspire.EnspireFile(tpath / "24well_clop0_95.csv")

ef3.wells, ef3._wells_platemap, ef3._platemap

(['A03', 'A04', 'A05', 'A06', 'B01', 'B02', 'C01', 'C02', 'C03'],
 ['A03', 'A04', 'A05', 'A06', 'B01', 'B02', 'C01', 'C02', 'C03'],
 [['A', '  ', '  ', '- ', '- ', '- ', '- '],
  ['B', '- ', '- ', '  ', '  ', '  ', '  '],
  ['C', '- ', '- ', '- ', '  ', '  ', '  '],
  ['D', '  ', '  ', '  ', '  ', '  ', '  ']])

ef1.__dict__.keys()

dict_keys(['file', 'verbose', 'metadata', 'measurements', 'wells', '_ini', '_fin', '_wells_platemap', '_platemap'])

ef1.measurements.keys(), ef2.measurements.keys()

(dict_keys(['A']), dict_keys(['B', 'A', 'C', 'D', 'E', 'F', 'G', 'H']))

when testing each spectra for the presence of a single wavelength in the appropriate monochromator

ef2.measurements["A"]["metadata"]

{'temp': '25',
 'Monochromator': 'Excitation',
 'Min wavelength': '400',
 'Max wavelength': '510',
 'Wavelength': '530',
 'Using of excitation filter': 'Top',
 'Measurement height': '8.9',
 'Number of flashes': '50',
 'Number of flashes integrated': '50',
 'Flash power': '100'}

ef2.measurements["A"].keys()

dict_keys(['metadata', 'lambda', 'F01', 'F02', 'F03', 'F04', 'F05', 'F06', 'F07'])

random.seed(11)
random.sample(ef1.measurements["A"]["F01"], 7)

[2163.0, 607.0, 1846.0, 517.0, 572.0, 2145.0, 2028.0]

fp = tpath / "h148g-spettroC-nota.csv"
n1 = prenspire.Note(fp, verbose=1)
n1._note.set_index("Well").loc["A01", ["Name", "Temp"]]

Wells ['A01', 'A02']...['G04', 'G05'] generated.

Name    H148G
Temp     20.0
Name: A01, dtype: object

n1.__dict__.keys()

dict_keys(['fpath', 'verbose', 'wells', '_note', 'titrations'])

n1.wells == ef1.wells, n1.wells == ef2.wells

(True, False)

n1.build_titrations(ef1)
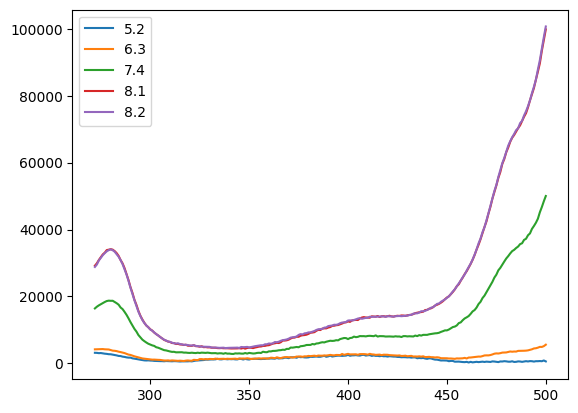
tit0 = n1.titrations["H148G"][20.0]["Cl_0.0"]["A"]
tit3 = n1.titrations["H148G"][20.0]["pH_7.4"]["A"]
tit0

	5.2	6.3	7.4	8.1	8.2
272.0	3151.0	4181.0	16413.0	29192.0	28816.0
273.0	3130.0	4204.0	16926.0	29909.0	29545.0
274.0	3043.0	4232.0	17331.0	30900.0	30750.0
275.0	3079.0	4283.0	17680.0	31717.0	31547.0
276.0	2975.0	4264.0	18020.0	32564.0	32336.0
...	...	...	...	...	...
496.0	636.0	4689.0	43230.0	87203.0	87842.0
497.0	683.0	4923.0	45173.0	89719.0	90666.0
498.0	632.0	4900.0	46725.0	93452.0	94101.0
499.0	854.0	5140.0	48452.0	96643.0	97506.0
500.0	573.0	5573.0	50025.0	99847.0	100715.0

229 rows × 5 columns

tit0.plot()
tit3.plot()

<Axes: >

ef = prenspire.EnspireFile(tpath / "G10.csv")
fp = tpath / "NTT-G10_note.csv"
nn = prenspire.Note(fp, verbose=1)
nn.build_titrations(ef)
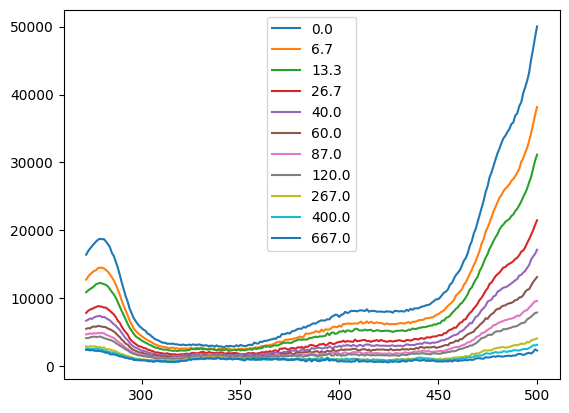
spectra = nn.titrations["NTT-G10"][20.0]["Cl_0.0"]["C"]

Wells ['D01', 'D02']...['G07', 'G08'] generated.

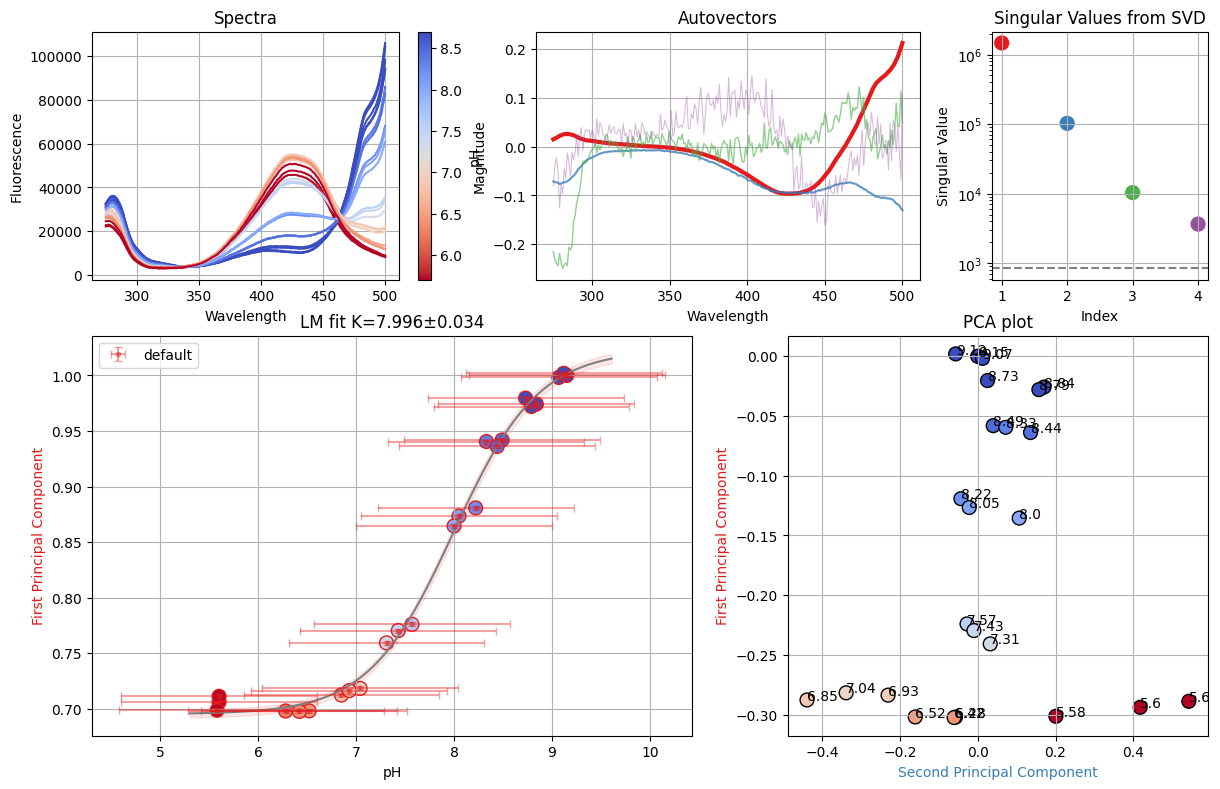
f_res = analyze_spectra(spectra, is_ph=True, band=None)
print(f_res.result.chisqr)
f_res.figure

551.9999999999978

def dataset_from_lres(lkey, lres, is_ph):
    data = {}
    for k, res in zip(lkey, lres, strict=False):
        x = res.mini.userargs[0]["default"].x
        y = res.mini.userargs[0]["default"].y
        data[k] = DataArray(x, y)
    return Dataset(data, is_ph=is_ph)


spectra_A = nn.titrations["NTT-G10"][20.0]["Cl_0.0"]["A"]
spectra_C = nn.titrations["NTT-G10"][20.0]["Cl_0.0"]["C"]
spectra_D = nn.titrations["NTT-G10"][20.0]["Cl_0.0"]["D"]

resA = analyze_spectra(spectra_A, is_ph=True, band=(466, 510))
resC = analyze_spectra(spectra_C, is_ph=True, band=(470, 500))
resD = analyze_spectra(spectra_D, is_ph=True, band=(450, 600))

ds_bands = dataset_from_lres(["A", "C", "D"], [resA, resC, resD], is_ph=True)

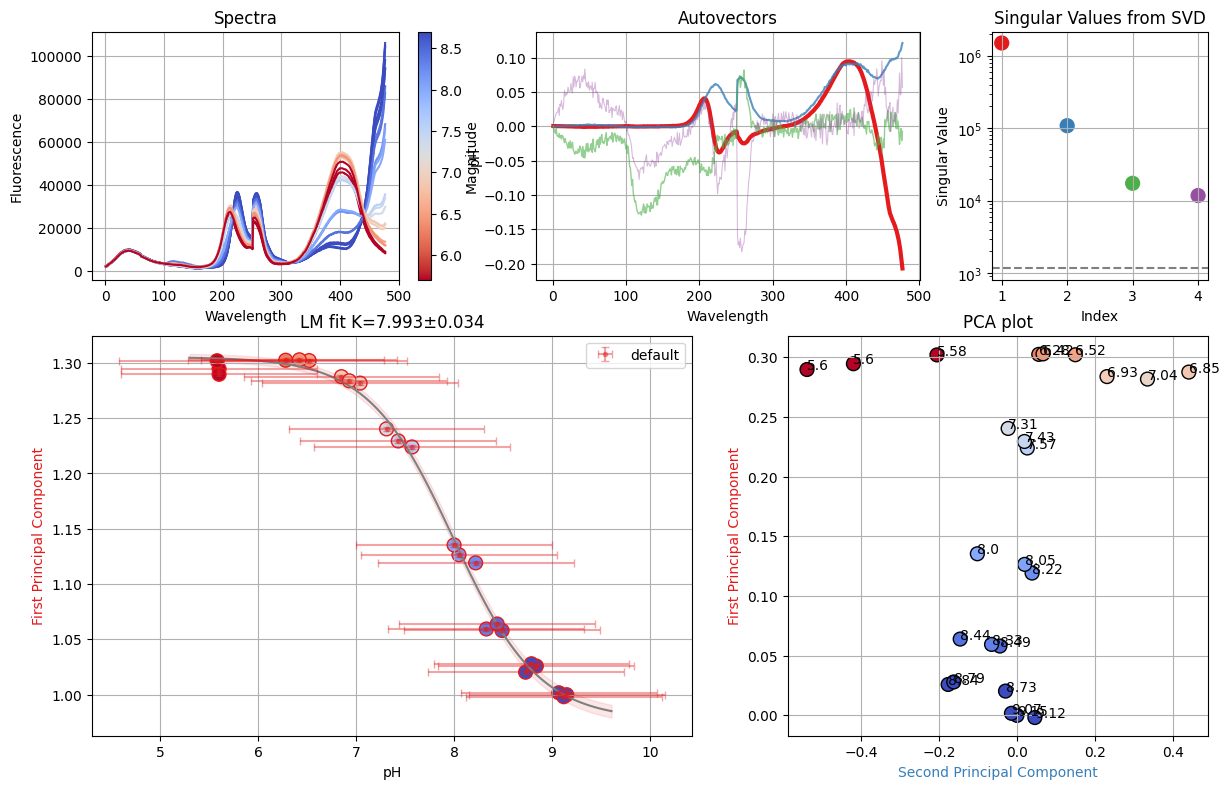
resA = analyze_spectra(spectra_A, is_ph=True)
resC = analyze_spectra(spectra_C, is_ph=True)
resD = analyze_spectra(spectra_D, is_ph=True)
ds_svd = dataset_from_lres(["A", "C", "D"], [resA, resC, resD], is_ph=True)

dbands = {"D": (466, 510)}
tit = nn.titrations["NTT-G10"][20.0]["Cl_0.0"]
sgres = analyze_spectra_glob(tit, ds_svd, dbands)

sgres.svd.figure

The chain is shorter than 50 times the integrated autocorrelation time for 1 parameter(s). Use this estimate with caution and run a longer chain!
N/50 = 108;
tau: [ 85.19893782 130.44068731  84.24663709  58.03314941  42.16063864]

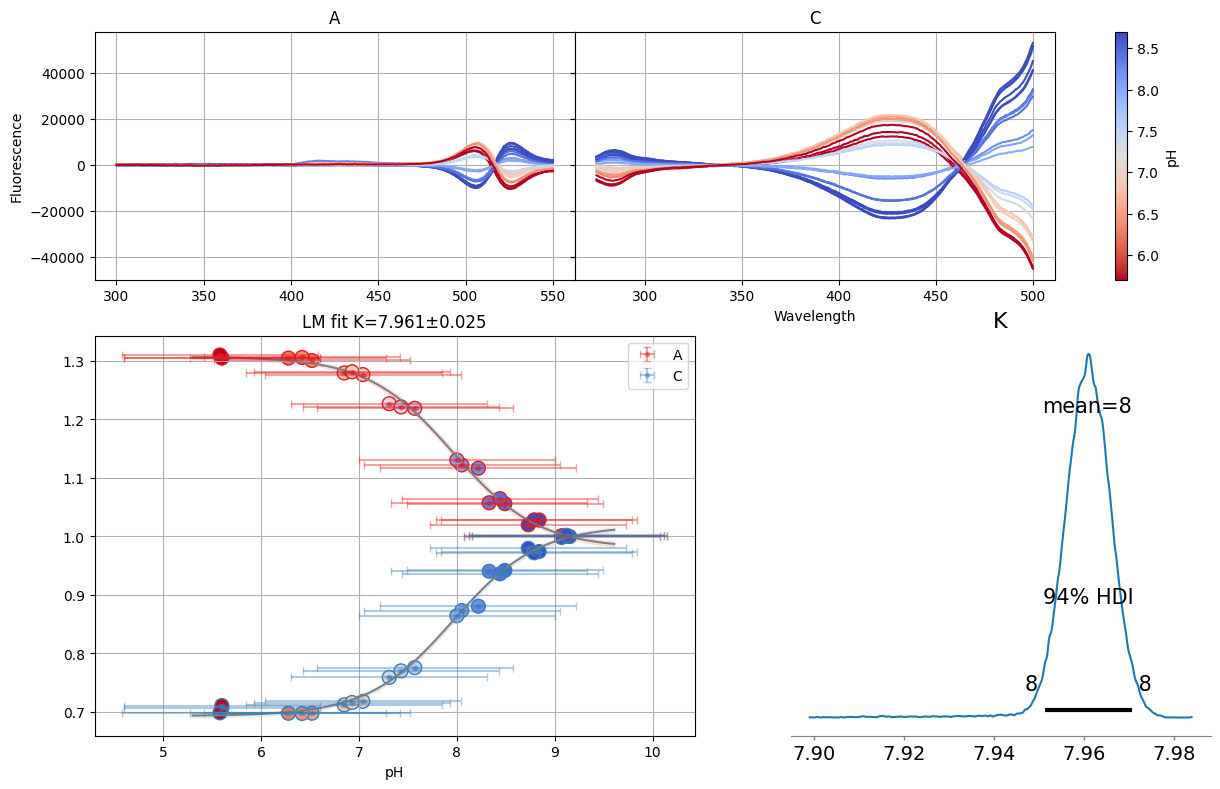
sgres.gsvd.figure

dbands = {"A": (466, 510), "C": (470, 500), "D": (450, 600)}
sgres = analyze_spectra_glob(nn.titrations["NTT-G10"][20.0]["Cl_0.0"], ds_bands, dbands)
sgres.bands.figure

The chain is shorter than 50 times the integrated autocorrelation time for 5 parameter(s). Use this estimate with caution and run a longer chain!
N/50 = 108;
tau: [245.25503923 285.78022353  54.0203079  245.68233136  76.78561808
 251.85092135 255.61380209]

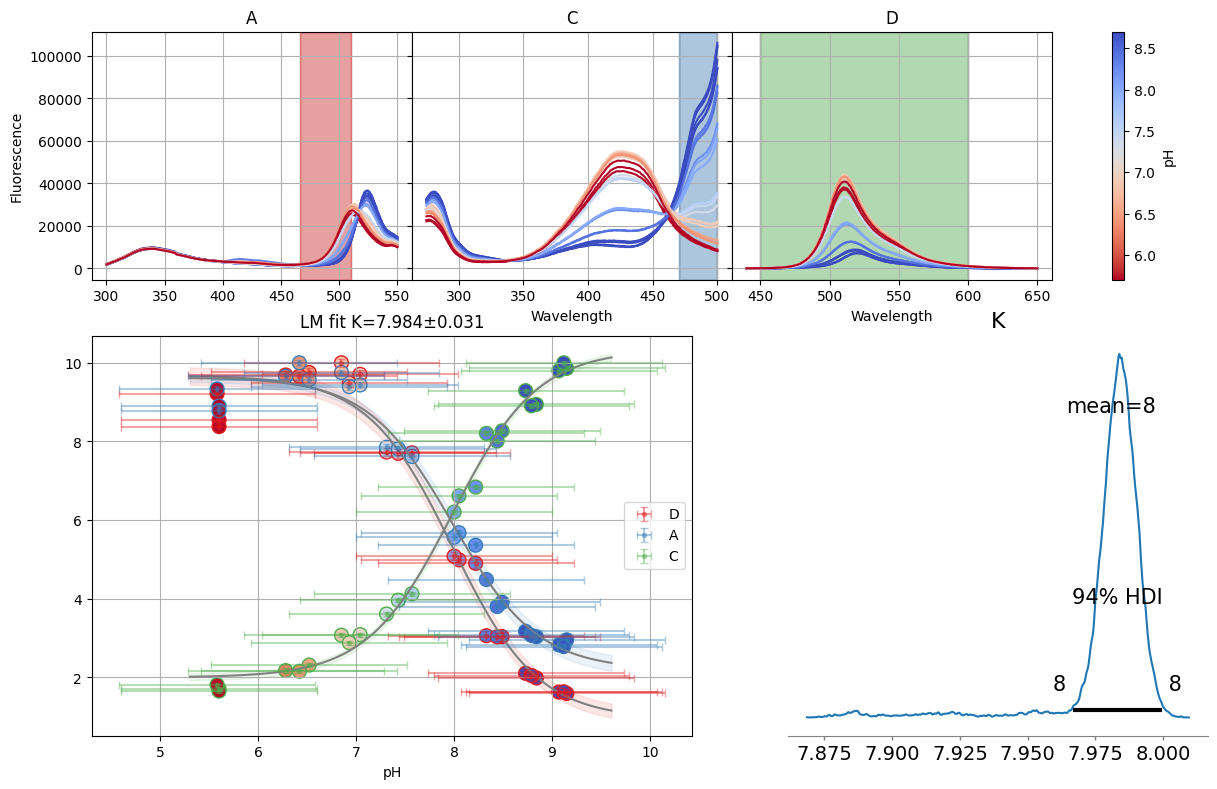
ci = lmfit.conf_interval(sgres.bands.mini, sgres.bands.result)
print(lmfit.ci_report(ci, ndigits=2, with_offset=False))

      99.73% 95.45% 68.27% _BEST_ 68.27% 95.45% 99.73%
 K   :   7.89   7.92   7.95   7.98   8.02   8.05   8.08
 S0_D:   0.21   0.47   0.72   0.96   1.19   1.42   1.67
 S1_D:   9.12   9.31   9.50   9.68   9.85  10.04  10.23
 S0_A:   1.65   1.84   2.02   2.20   2.37   2.54   2.72
 S1_A:   9.23   9.37   9.50   9.63   9.76   9.89  10.03
 S0_C:   9.90  10.05  10.19  10.33  10.47  10.62  10.79
 S1_C:   1.70   1.81   1.91   2.00   2.10   2.19   2.29

weight_multi_ds_titration(ds_svd)
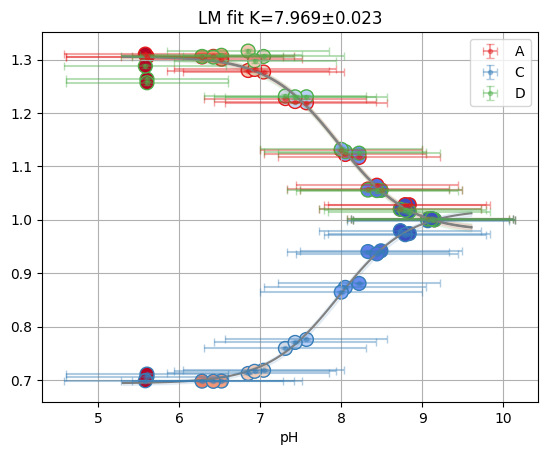
res = fit_binding_glob(ds_svd)
res.figure

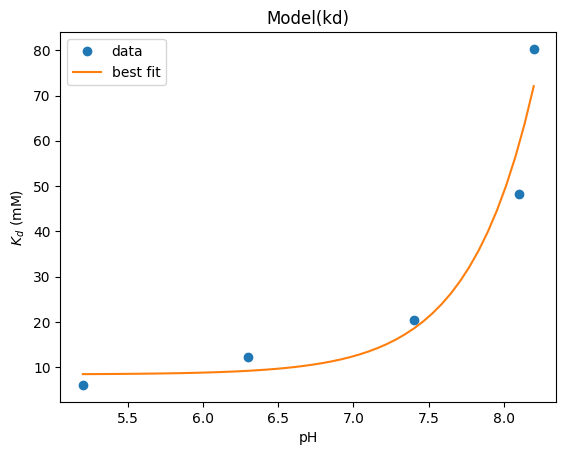
xx = np.array([5.2, 6.3, 7.4, 8.1, 8.2])
yy = np.array([6.05, 12.2, 20.38, 48.2, 80.3])


def kd(x, kd1, pka):
    return kd1 * (1 + 10 ** (pka - x)) / 10 ** (pka - x)


model = lmfit.Model(kd)
params = lmfit.Parameters()
params.add("kd1", value=10.0)
params.add("pka", value=6.6)
result = model.fit(yy, params, x=xx)

result.plot_fit(numpoints=50, ylabel="$K_d$ (mM)", xlabel="pH")

<Axes: title={'center': 'Model(kd)'}, xlabel='pH', ylabel='$K_d$ (mM)'>

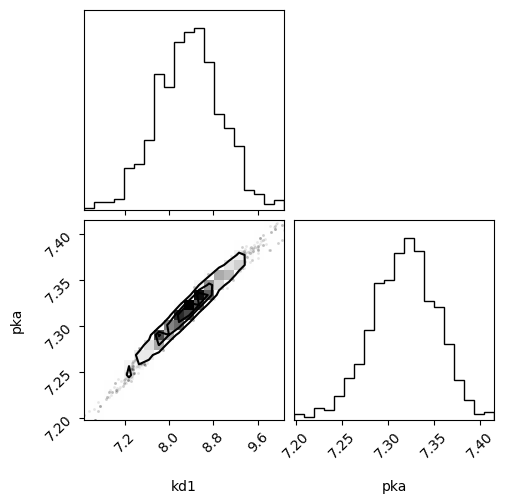
import os

result_emcee = result.emcee(
    steps=int(os.environ.get("CLOPHFIT_DOCS_EMCEE_STEPS", "1800")),
    burn=int(os.environ.get("CLOPHFIT_DOCS_EMCEE_BURN", "150")),
    workers=int(os.environ.get("CLOPHFIT_EMCEE_WORKERS", "1")),
    nwalkers=int(os.environ.get("CLOPHFIT_DOCS_EMCEE_NWALKERS", "10")),
    seed=1,
    progress=False,
)
fig = plot_emcee(result_emcee.flatchain)

The chain is shorter than 50 times the integrated autocorrelation time for 2 parameter(s). Use this estimate with caution and run a longer chain!
N/50 = 6;
tau: [21.09140903 21.25484981]

import pymc as pm

# Assuming x_data and y_data are your data
with pm.Model() as model:
    kd1 = pm.Normal(
        "kd1", mu=result.params["kd1"].value, sigma=result.params["kd1"].stderr
    )
    pka = pm.Normal(
        "pka", mu=result.params["pka"].value, sigma=result.params["pka"].stderr
    )

    y_pred = pm.Deterministic("y_pred", kd(xx, kd1, pka))

    likelihood = pm.Normal("y", mu=y_pred, sigma=1, observed=yy)

    trace = pm.sample(1000, tune=2000, random_seed=1, chains=8, cores=8)

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (8 chains in 8 jobs)

NUTS: [kd1, pka]

/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.14/site-packages/pymc/step_methods/hmc/quadpotential.py:316: RuntimeWarning: overflow encountered in dot
  return 0.5 * np.dot(x, v_out)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.14/site-packages/pymc/step_methods/hmc/quadpotential.py:316: RuntimeWarning: overflow encountered in dot
  return 0.5 * np.dot(x, v_out)

Sampling 8 chains for 2_000 tune and 1_000 draw iterations (16_000 + 8_000 draws total) took 28 seconds.

The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details

pm.model_to_graphviz(model)

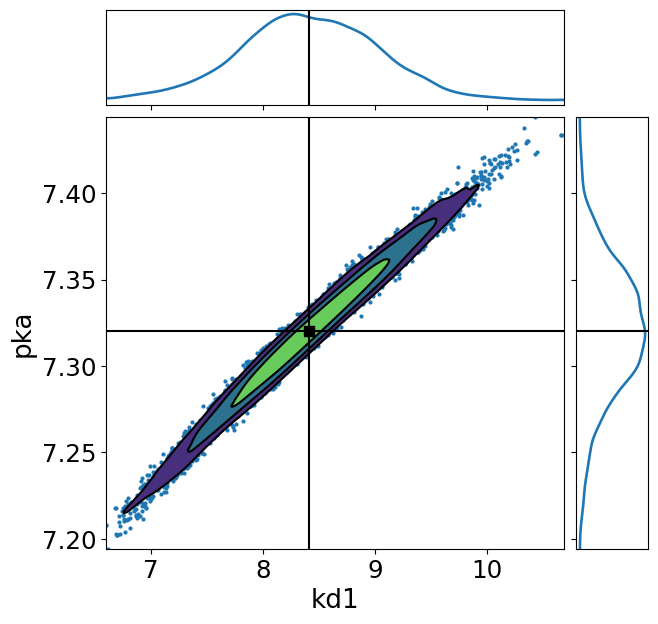
import arviz as az

ax = az.plot_pair(
    trace,
    divergences=1,
    var_names=["kd1", "pka"],
    kind=["kde", "scatter"],
    kde_kwargs={"fill_last": False},
    marginals=True,
    point_estimate="mean",
    figsize=(7, 7),
)

import corner

# Extract the posterior samples for the parameters of interest
kd1_samples = trace.posterior["kd1"].to_numpy().flatten()
pka_samples = trace.posterior["pka"].to_numpy().flatten()
# Ensure the samples are in the correct format for the corner plotpm.plot_posterior(trace, var_names=["R0", "R1", "K"])
samples_array = np.column_stack([kd1_samples, pka_samples])
# Plot the corner plot
f = corner.corner(samples_array, labels=["kd1", "pka"])

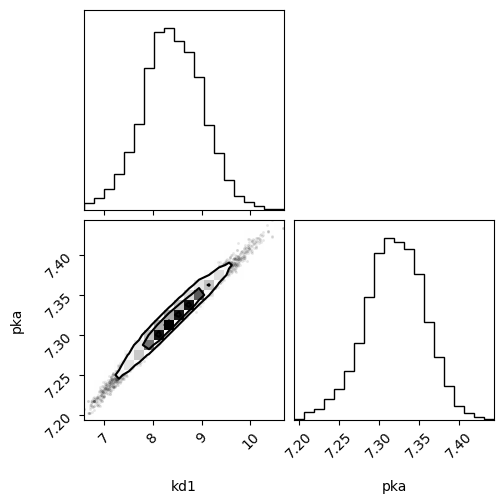
pm.plot_trace(trace, rug=True)

array([[<Axes: title={'center': 'kd1'}>, <Axes: title={'center': 'kd1'}>],
       [<Axes: title={'center': 'pka'}>, <Axes: title={'center': 'pka'}>],
       [<Axes: title={'center': 'y_pred'}>,
        <Axes: title={'center': 'y_pred'}>]], dtype=object)

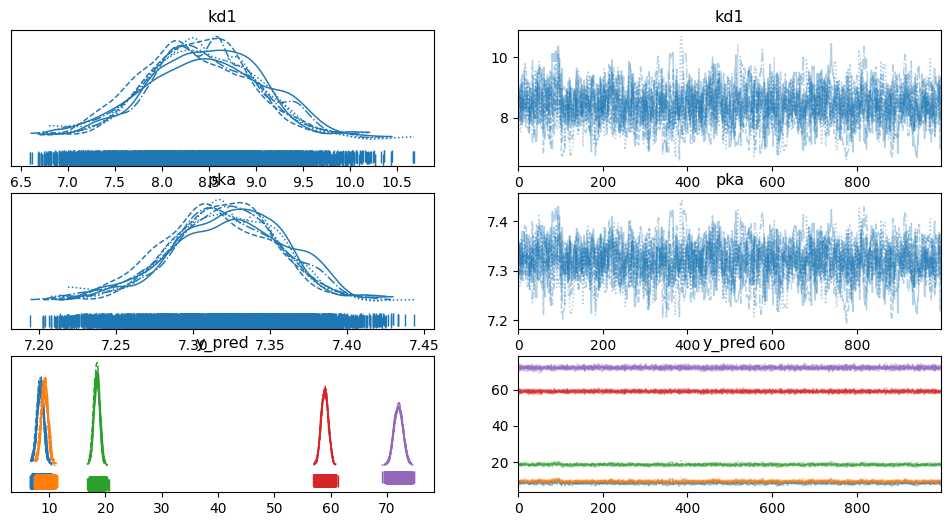
pm.plot_posterior(trace, var_names=["kd1", "pka"])

array([<Axes: title={'center': 'kd1'}>, <Axes: title={'center': 'pka'}>],
      dtype=object)

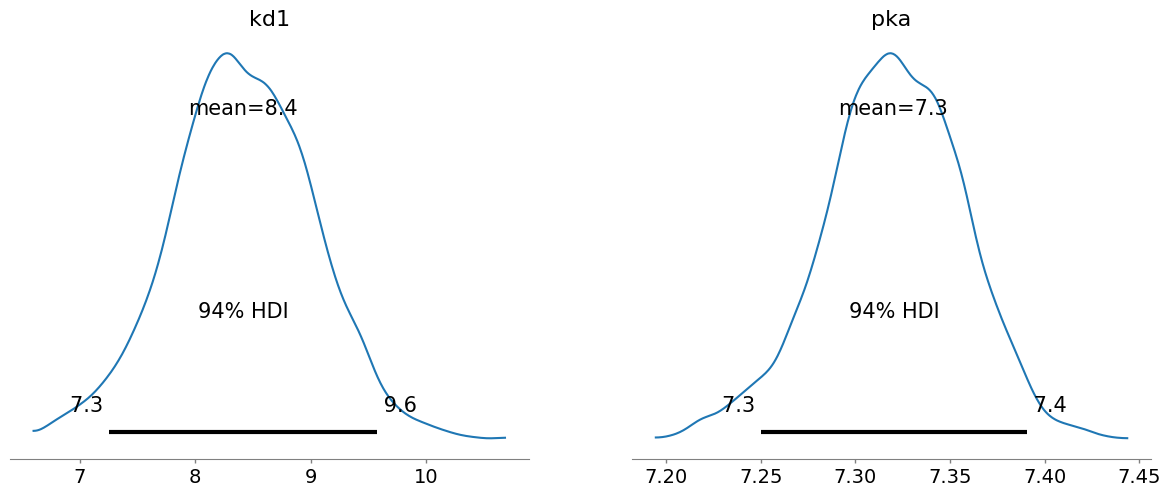
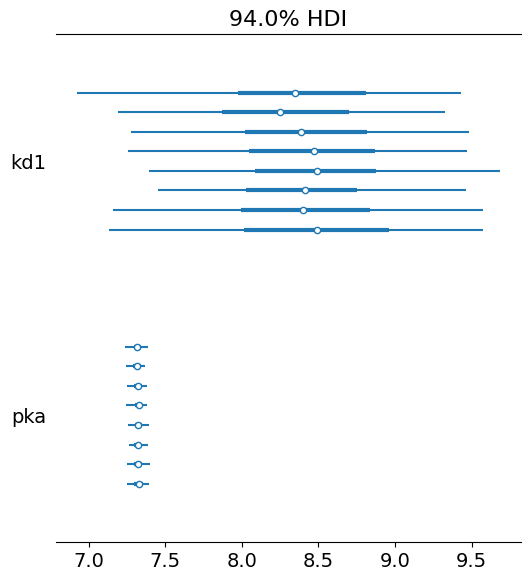
pm.plot_forest(trace, var_names=["kd1", "pka"])
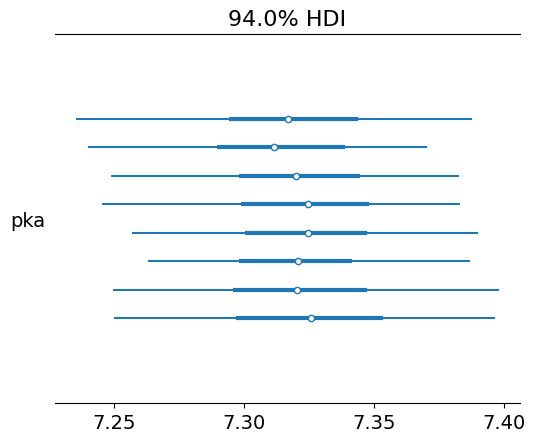
pm.plot_forest(trace, var_names=["pka"])

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)