2. prtecan Tutorial

This tutorial demonstrates how to process Tecan plate reader data using the clophfit.prtecan module.

What you’ll learn:

• Tecan file structure and label blocks

• Building titrations from multiple files (manually and from list file)

• Setting plate scheme, loading additions, background handling

• Inspecting and plotting results

• Brief overview of fitting methods and quality control

# Setup
%load_ext autoreload
%autoreload 2

from pathlib import Path

import arviz as az
import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline

from clophfit import prtecan

# Point to the tests data directory shipped with the repo
data_root = Path("../../tests/Tecan")
l1_dir = data_root / "L1"
l2_dir = data_root / "140220"  # second dataset used by the original tutorial
l4_dir = data_root / "L4"

2.1. 1) Understanding Tecan file structure

Each Tecan file contains global metadata and one or more label blocks (measurement blocks). Blocks with identical key metadata are equivalent; blocks differing only by Integration Time, Flashes, or Gain are almost equivalent after normalization.

# Load a single Tecan file and inspect label blocks
tf = prtecan.Tecanfile(l1_dir / "290513_7.2.xls")
lb1, lb2 = tf.labelblocks[1], tf.labelblocks[2]
print("Available label blocks:", list(tf.labelblocks.keys()))
lb1.metadata

Available label blocks: [1, 2]

{'Label': Metadata(value='Label1', unit=None),
 'Mode': Metadata(value='Fluorescence Top Reading', unit=None),
 'Excitation Wavelength': Metadata(value=400, unit=['nm']),
 'Emission Wavelength': Metadata(value=535, unit=['nm']),
 'Excitation Bandwidth': Metadata(value=20, unit=['nm']),
 'Emission Bandwidth': Metadata(value=25, unit=['nm']),
 'Gain': Metadata(value=94, unit=['Manual']),
 'Number of Flashes': Metadata(value=10, unit=None),
 'Integration Time': Metadata(value=20, unit=['µs']),
 'Lag Time': Metadata(value='µs', unit=None),
 'Settle Time': Metadata(value='ms', unit=None),
 'Start Time:': Metadata(value='29/05/2013 12.28.10', unit=None),
 'Temperature': Metadata(value=24.9, unit=['°C']),
 'End Time:': Metadata(value='29/05/2013 12.28.50', unit=None)}

print("\nSample Data (A01-B06):")
print({k: v for i, (k, v) in enumerate(lb2.data.items()) if i < 18})

Sample Data (A01-B06):
{'A01': 8761.0, 'A02': 15316.0, 'A03': 14346.0, 'A04': 8474.0, 'A05': 16319.0, 'A06': 10912.0, 'A07': 10855.0, 'A08': 12565.0, 'A09': 16695.0, 'A10': 12125.0, 'A11': 10895.0, 'A12': 36597.0, 'B01': 10280.0, 'B02': 11124.0, 'B03': 19612.0, 'B04': 10109.0, 'B05': 11239.0, 'B06': 8556.0}

Load additional files to compare block equivalence and demonstrate normalization across Gain differences.

tf1 = prtecan.Tecanfile(l1_dir / "290513_5.5.xls")  # two equivalent blocks
tf2 = prtecan.Tecanfile(
    l1_dir / "290513_8.8.xls"
)  # one equivalent, one almost equivalent

print("tf.lb1 = tf2.lb1 (strict):", lb1 == tf2.labelblocks[1])
print("tf.lb2 = tf2.lb2 (strict):", lb2 == tf2.labelblocks[2])
print("tf.lb2 ~ tf2.lb2 (almost):", lb2.almost_equal(tf2.labelblocks[2]))

tf.lb1 = tf2.lb1 (strict): True
tf.lb2 = tf2.lb2 (strict): False
tf.lb2 ~ tf2.lb2 (almost): True

2.2. 2) Grouping files: manual and convenience constructor

You can group equivalent blocks across files either via TecanfilesGroup or by constructing a Titration directly.

# Manual grouping
tfg = prtecan.TecanfilesGroup([tf2, tf, tf1])
lbg1 = tfg.labelblocksgroups[1]
print("Well A01 raw:", lbg1.data["A01"])
print("Well A01 normalized:", lbg1.data_nrm["A01"])

# Same using Titration with explicit x (e.g., pH values)
tit_manual = prtecan.Titration([tf2, tf, tf1], x=np.array([8.8, 7.2, 5.5]), is_ph=True)
print(tit_manual)
print("A01 normalized via Titration:", tit_manual.labelblocksgroups[1].data_nrm["A01"])
tit_manual.labelblocksgroups == tfg.labelblocksgroups

Different LabelblocksGroup across files: ['../../tests/Tecan/L1/290513_8.8.xls', '../../tests/Tecan/L1/290513_7.2.xls', '../../tests/Tecan/L1/290513_5.5.xls'].
Different LabelblocksGroup across files: ['../../tests/Tecan/L1/290513_8.8.xls', '../../tests/Tecan/L1/290513_7.2.xls', '../../tests/Tecan/L1/290513_5.5.xls'].

Well A01 raw: [17123.0, 17088.0, 18713.0]
Well A01 normalized: [910.7978723404256, 908.936170212766, 995.3723404255319]
Titration
        files=["../../tests/Tecan/L1/290513_8.8.xls", ...],
        x=[np.float64(8.8), np.float64(7.2), np.float64(5.5)],
        x_err=[],
        labels=dict_keys([1, 2]),
        params=TitrationConfig(bg=True, bg_adj=False, dil=True, nrm=True, bg_mth='mean', mcmc='None')   pH=True additions=[]
        scheme=PlateScheme(file=None, _buffer=[], _discard=[], _ctrl=[], _names={}))
A01 normalized via Titration: [910.7978723404256, 908.936170212766, 995.3723404255319]

True

2.3. 3) Build a titration from a list file

Using a list file is convenient and less error-prone. The example list/plate files are in tests/Tecan/L1.

tit = prtecan.Titration.fromlistfile(l1_dir / "list.pH.csv", is_ph=True)
print("x values (e.g., pH):", tit.x)
lbg1 = tit.labelblocksgroups[1]
lbg2 = tit.labelblocksgroups[2]
print(
    "Temperature in labelblocksgroup 2:",
    [lb.metadata.get("Temperature").value for lb in lbg2.labelblocks],
    lbg2.labelblocks[5].metadata.get("Temperature").unit[0],
)
(lbg1.metadata, lbg2.metadata)

Different LabelblocksGroup across files: ['../../tests/Tecan/L1/290513_8.8.xls', '../../tests/Tecan/L1/290513_8.2.xls', '../../tests/Tecan/L1/290513_7.7.xls', '../../tests/Tecan/L1/290513_7.2.xls', '../../tests/Tecan/L1/290513_6.6.xls', '../../tests/Tecan/L1/290513_6.1.xls', '../../tests/Tecan/L1/290513_5.5.xls'].

x values (e.g., pH): [8.9  8.3  7.7  7.05 6.55 6.   5.5 ]
Temperature in labelblocksgroup 2: [25.1, 24.9, 24.7, 24.7, 25.1, 25.1, 25.1] °C

({'Label': Metadata(value='Label1', unit=None),
  'Mode': Metadata(value='Fluorescence Top Reading', unit=None),
  'Excitation Wavelength': Metadata(value=400, unit=['nm']),
  'Emission Wavelength': Metadata(value=535, unit=['nm']),
  'Excitation Bandwidth': Metadata(value=20, unit=['nm']),
  'Emission Bandwidth': Metadata(value=25, unit=['nm']),
  'Number of Flashes': Metadata(value=10, unit=None),
  'Integration Time': Metadata(value=20, unit=['µs']),
  'Lag Time': Metadata(value='µs', unit=None),
  'Settle Time': Metadata(value='ms', unit=None),
  'Gain': Metadata(value=94, unit=None)},
 {'Label': Metadata(value='Label2', unit=None),
  'Mode': Metadata(value='Fluorescence Top Reading', unit=None),
  'Excitation Wavelength': Metadata(value=485, unit=['nm']),
  'Emission Wavelength': Metadata(value=535, unit=['nm']),
  'Excitation Bandwidth': Metadata(value=25, unit=['nm']),
  'Emission Bandwidth': Metadata(value=25, unit=['nm']),
  'Number of Flashes': Metadata(value=10, unit=None),
  'Integration Time': Metadata(value=20, unit=['µs']),
  'Lag Time': Metadata(value='µs', unit=None),
  'Settle Time': Metadata(value='ms', unit=None),
  'Movement': Metadata(value='Move Plate Out', unit=None)})

Within each label-block group, normalized data (by Gain, Flashes, Integration Time) are readily available. In the case of not fully identical labelblock metadata non-normalized data might not exist (empty dict {}).

# Inspect raw vs normalized for a sample well
well = "H03"
(lbg1.data[well], lbg2.data, lbg1.data_nrm[well], lbg2.data_nrm[well])

([27593.0, 26956.0, 26408.0, 26815.0, 28308.0, 30227.0, 30640.0],
 {},
 [1467.712765957447,
  1433.8297872340427,
  1404.6808510638298,
  1426.3297872340427,
  1505.7446808510638,
  1607.8191489361702,
  1629.787234042553],
 [1456.2121212121212,
  1363.9285714285716,
  1310.357142857143,
  1214.5408163265306,
  1200.9693877551022,
  1224.642857142857,
  1193.8265306122448])

2.4. 4) Load plate scheme and additions

The plate scheme defines buffer and control wells; additions define dilution steps. After loading these, the processed tit.data[...] arrays reflect background subtraction and optional dilution correction, depending on tit.params.

# Load plate scheme and additions (kept to L1 files for consistency)
tit.load_scheme(l1_dir / "scheme.txt")
print(
    f"Titration with {len(tit.tecanfiles)} files and {len(tit.labelblocksgroups)} label groups"
)
print("Buffer wells:", tit.scheme.buffer)
print("Control wells:", tit.scheme.ctrl)
print("Named groups:", tit.scheme.names)

tit.load_additions(l1_dir / "additions.pH")
print("Additions:", tit.additions)
tit.params.bg_adj = True
tit.params.bg_mth = "meansd"
print("Titration Params:", tit.params)
# Example: compare values in data vs normalized groups (after scheme/additions)
(lbg1.data["H12"], tit.data[1]["H12"], lbg1.data_nrm["H12"], tit.bg[1])

Buffer for 'D05:1' was adjusted by 0.74 SD.
Buffer for 'E02:1' was adjusted by 1.18 SD.
Buffer for 'F05:1' was adjusted by 0.52 SD.
Buffer for 'G05:1' was adjusted by 0.60 SD.
Buffer for 'D08:1' was adjusted by 0.56 SD.
Buffer for 'G04:1' was adjusted by 0.79 SD.
Buffer for 'B02:1' was adjusted by 1.27 SD.
Buffer for 'B10:1' was adjusted by 0.08 SD.
Buffer for 'C06:1' was adjusted by 1.38 SD.
Buffer for 'F03:1' was adjusted by 0.33 SD.
Buffer for 'C05:1' was adjusted by 0.94 SD.
Buffer for 'D04:1' was adjusted by 1.29 SD.
Buffer for 'D07:1' was adjusted by 0.53 SD.
Buffer for 'E07:1' was adjusted by 0.89 SD.
Buffer for 'B08:1' was adjusted by 0.81 SD.
Buffer for 'D02:1' was adjusted by 3.31 SD.
Buffer for 'A06:1' was adjusted by 0.66 SD.
Buffer for 'E09:1' was adjusted by 0.09 SD.
Buffer for 'B01:1' was adjusted by 1.78 SD.
Buffer for 'A04:1' was adjusted by 1.53 SD.
Buffer for 'B06:1' was adjusted by 1.31 SD.
Buffer for 'F07:1' was adjusted by 0.13 SD.
Buffer for 'G08:1' was adjusted by 0.97 SD.

Titration with 7 files and 2 label groups
Buffer wells: ['C12', 'D01', 'D12', 'E01', 'E12', 'F01']
Control wells: ['B12', 'H01', 'A12', 'G01', 'F12', 'B01', 'C01']
Named groups: {'E2GFP': {'C01', 'G01', 'F12', 'B12'}, 'V224L': {'H01', 'A12'}, 'V224Q': {'B01'}}
Additions: [100, 2, 2, 2, 2, 2, 2]
Titration Params: TitrationConfig(bg=True, bg_adj=True, dil=True, nrm=True, bg_mth='meansd', mcmc='None')

Buffer for 'E04:1' was adjusted by 1.22 SD.
Buffer for 'C02:1' was adjusted by 5.47 SD.
Buffer for 'A02:1' was adjusted by 2.10 SD.
Buffer for 'C09:1' was adjusted by 0.48 SD.
Buffer for 'C04:1' was adjusted by 2.42 SD.
Buffer for 'E03:1' was adjusted by 2.30 SD.
Buffer for 'D03:1' was adjusted by 2.13 SD.
Buffer for 'F02:1' was adjusted by 2.00 SD.
Buffer for 'C03:1' was adjusted by 4.13 SD.
Buffer for 'G02:1' was adjusted by 1.82 SD.
Buffer for 'H09:1' was adjusted by 0.67 SD.
Buffer for 'C01:1' was adjusted by 6.03 SD.
Buffer for 'H10:1' was adjusted by 0.40 SD.
Buffer for 'F09:1' was adjusted by 0.35 SD.
Buffer for 'E05:1' was adjusted by 0.44 SD.
Buffer for 'H01:1' was adjusted by 2.24 SD.
Buffer for 'B05:1' was adjusted by 0.72 SD.
Buffer for 'B04:1' was adjusted by 1.78 SD.
Buffer for 'H07:1' was adjusted by 0.62 SD.
Buffer for 'E08:1' was adjusted by 0.59 SD.
Buffer for 'D09:1' was adjusted by 0.44 SD.
Buffer for 'A03:1' was adjusted by 1.51 SD.
Buffer for 'A07:1' was adjusted by 1.89 SD.
Buffer for 'D05:2' was adjusted by 1.72 SD.
Buffer for 'E02:2' was adjusted by 1.67 SD.
Buffer for 'G05:2' was adjusted by 0.74 SD.
Buffer for 'D08:2' was adjusted by 1.49 SD.
Buffer for 'B02:2' was adjusted by 1.46 SD.
Buffer for 'B10:2' was adjusted by 0.91 SD.
Buffer for 'C06:2' was adjusted by 1.91 SD.
Buffer for 'C05:2' was adjusted by 1.03 SD.
Buffer for 'D04:2' was adjusted by 1.28 SD.
Buffer for 'D07:2' was adjusted by 0.97 SD.
Buffer for 'E07:2' was adjusted by 1.98 SD.
Buffer for 'B08:2' was adjusted by 1.52 SD.
Buffer for 'D02:2' was adjusted by 2.65 SD.
Buffer for 'A06:2' was adjusted by 1.60 SD.
Buffer for 'B01:2' was adjusted by 2.60 SD.
Buffer for 'A04:2' was adjusted by 2.37 SD.
Buffer for 'B06:2' was adjusted by 1.96 SD.
Buffer for 'G08:2' was adjusted by 1.08 SD.
Buffer for 'E04:2' was adjusted by 1.99 SD.
Buffer for 'C02:2' was adjusted by 7.26 SD.
Buffer for 'A02:2' was adjusted by 1.52 SD.
Buffer for 'C09:2' was adjusted by 1.09 SD.
Buffer for 'C04:2' was adjusted by 2.62 SD.
Buffer for 'E03:2' was adjusted by 3.11 SD.
Buffer for 'D03:2' was adjusted by 2.29 SD.
Buffer for 'F02:2' was adjusted by 1.85 SD.
Buffer for 'C03:2' was adjusted by 5.86 SD.
Buffer for 'G02:2' was adjusted by 1.96 SD.
Buffer for 'C01:2' was adjusted by 8.08 SD.
Buffer for 'B11:2' was adjusted by 0.61 SD.
Buffer for 'E05:2' was adjusted by 1.69 SD.
Buffer for 'H01:2' was adjusted by 2.03 SD.
Buffer for 'B05:2' was adjusted by 1.11 SD.
Buffer for 'B04:2' was adjusted by 2.00 SD.
Buffer for 'H07:2' was adjusted by 1.34 SD.
Buffer for 'E08:2' was adjusted by 1.59 SD.
Buffer for 'D09:2' was adjusted by 0.77 SD.
Buffer for 'A03:2' was adjusted by 2.15 SD.
Buffer for 'A07:2' was adjusted by 2.59 SD.

([28309.0, 27837.0, 26511.0, 25771.0, 27048.0, 27794.0, 28596.0],
 array([302.45567376, 321.23670213, 313.92695035, 277.94929078,
        353.65212766, 335.1001773 , 316.34042553]),
 [1505.7978723404256,
  1480.6914893617022,
  1410.159574468085,
  1370.7978723404256,
  1438.723404255319,
  1478.404255319149,
  1521.063829787234],
 array([1203.34219858, 1165.7535461 , 1108.30673759, 1108.58156028,
        1111.2677305 , 1173.7677305 , 1238.61702128]))

Background handling summary:

• labelblocksgroups[:].data: unchanged raw block data

• labelblocksgroups[:].data_buffersubtracted: background-subtracted

• tit.data: background-subtracted and dilution-corrected (if enabled)

The order in which you apply dilution correction and plate scheme can impact your intermediate results, even though the final results might be the same.

Dilution correction adjusts the measured data to account for any dilutions made during sample preparation. This typically involves multiplying the measured values by the dilution factor to estimate the true concentration of the sample.

A plate scheme describes the layout of the samples on a plate (common in laboratory experiments, such as those involving microtiter plates). The plate scheme may involve rearranging or grouping the data in some way based on the physical location of the samples on the plate.

# Demonstrate changing background wells and seeing bg estimate
import copy

tit2 = copy.deepcopy(tit)
tit2.params.bg = True
tit2.buffer.wells = ["D01", "E01"]
tit.bg, tit2.bg

({1: array([1203.34219858, 1165.7535461 , 1108.30673759, 1108.58156028,
         1111.2677305 , 1173.7677305 , 1238.61702128]),
  2: array([505.62289562, 467.14285714, 473.48639456, 500.29761905,
         524.3622449 , 584.3452381 , 581.8962585 ])},
 {1: array([1016.62234043,  971.56914894,  937.9787234 ,  951.38297872,
          985.74468085, 1005.26595745, 1070.85106383]),
  2: array([420.05050505, 364.69387755, 382.5255102 , 402.19387755,
         430.84183673, 455.07653061, 466.19897959])})

2.5. 5) Quick look at fitting and results

The tit.results container provides per-label fits; tit.result_global combines multiple labels. Below we only preview access/plotting. For advanced Bayesian/ODR methods, see the dedicated section.

tit.bg_err

{1: array([85.42617933, 85.42617933, 85.42617933, 85.42617933, 85.42617933,
        85.42617933, 85.42617933]),
 2: array([54.27412064, 54.27412064, 54.27412064, 54.27412064, 54.27412064,
        54.27412064, 54.27412064])}

# Access result objects and figures
well = "D10"
single1 = tit.results[1][well]
single2 = tit.results[2][well]
glob = tit.result_global[well]
odr = tit.result_odr[well]

# Display figures inline
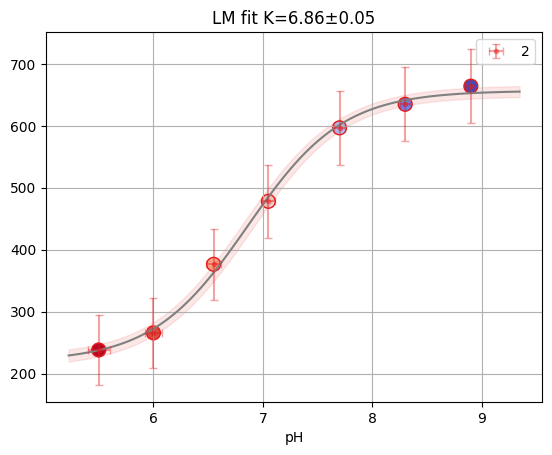
print(f"Reduced X2: {single2.result.redchi:.3f}")
single2.figure

Reduced X2: 0.034

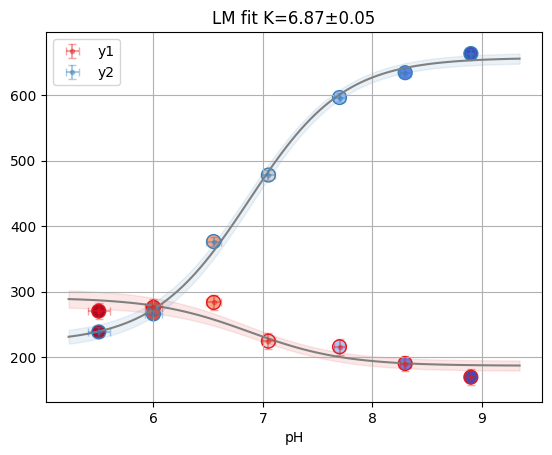
print(f"Reduced X2: {glob.result.redchi:.3f}")
glob.figure

Reduced X2: 2.259

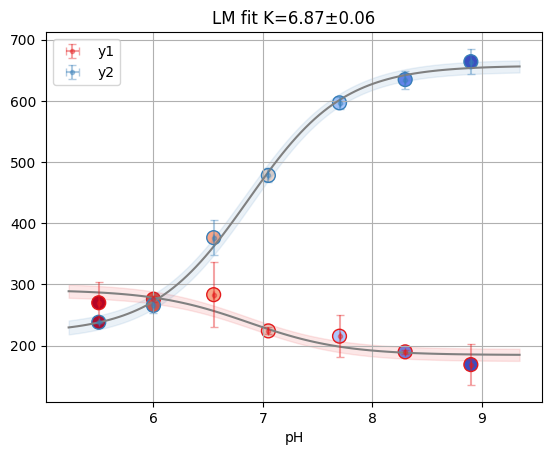
print(f"Reduced X2: {odr.mini.sum_square:.3f}")
odr.figure

Reduced X2: 0.007

tit.results[1].dataframe.head()

	K	sK	Khdi03	Khdi97	S0_1	sS0_1	S0_1hdi03	S0_1hdi97	S1_1	sS1_1	S1_1hdi03	S1_1hdi97
well
D10	7.353784	0.306455	3	11	173.607145	13.702403	-inf	inf	279.017836	11.34187	-inf	inf

%%time rro = fitting.fit_binding_pymc_odr(glob, n_sd=0.5) rrodf = az.summary(rro) dfaz.plot_trace(rro)

tit.result_mcmc

outlier in F11: [1 1 1 0 1 1 1 1 1 1 1 1 1 1].

{}

tit.result_multi_mcmc

{}

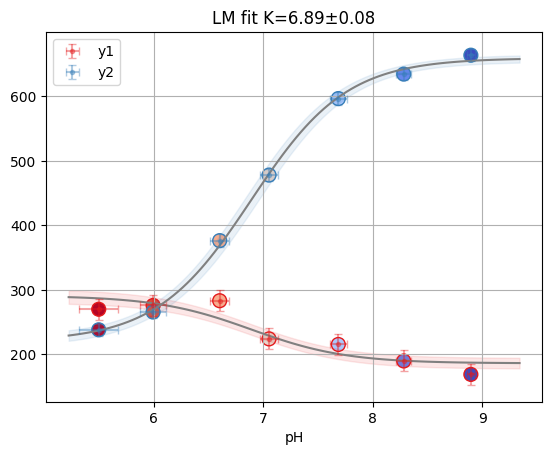
rp = tit.result_mcmc[well]
rp.figure

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [K, S0_y1, S1_y1, S0_y2, S1_y2, x_diff, x_start, ye_mag]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 18 seconds.

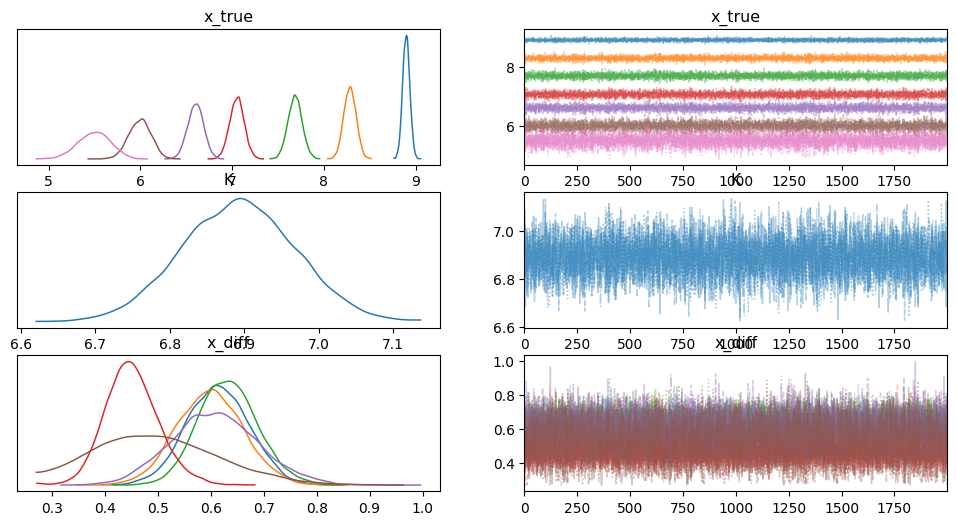
az.plot_trace(
    rp.mini, var_names=["x_true", "K", "x_diff"], divergences=False, combined=True
)

array([[<Axes: title={'center': 'x_true'}>,
        <Axes: title={'center': 'x_true'}>],
       [<Axes: title={'center': 'K'}>, <Axes: title={'center': 'K'}>],
       [<Axes: title={'center': 'x_diff'}>,
        <Axes: title={'center': 'x_diff'}>]], dtype=object)

# 5.1 Bayesian fitting with PyMC
tit.params.mcmc = "single"
result_mcmc = tit.result_mcmc[well]

print("MCMC Results:")
print(f"Kd: {result_mcmc.result.params['K'].value:.2f}")
print(
    f"95% HDI: [{result_mcmc.result.params['K'].min:.2f}, {result_mcmc.result.params['K'].max:.2f}]"
)

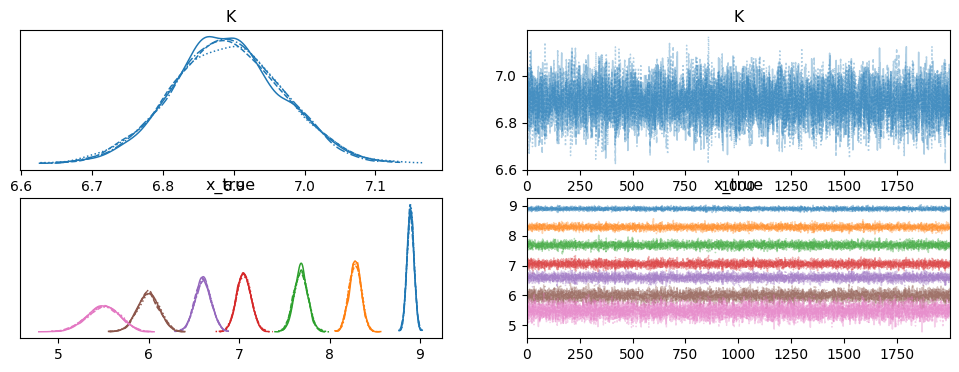
# Plot trace
az.plot_trace(result_mcmc.mini, var_names=["K", "x_true"]);

Buffer for 'D05:1' was adjusted by 0.74 SD.
Buffer for 'E02:1' was adjusted by 1.18 SD.
Buffer for 'F05:1' was adjusted by 0.52 SD.
Buffer for 'G05:1' was adjusted by 0.60 SD.
Buffer for 'D08:1' was adjusted by 0.56 SD.
Buffer for 'G04:1' was adjusted by 0.79 SD.
Buffer for 'B02:1' was adjusted by 1.27 SD.
Buffer for 'B10:1' was adjusted by 0.08 SD.
Buffer for 'C06:1' was adjusted by 1.38 SD.
Buffer for 'F03:1' was adjusted by 0.33 SD.
Buffer for 'C05:1' was adjusted by 0.94 SD.
Buffer for 'D04:1' was adjusted by 1.29 SD.
Buffer for 'D07:1' was adjusted by 0.53 SD.
Buffer for 'E07:1' was adjusted by 0.89 SD.
Buffer for 'B08:1' was adjusted by 0.81 SD.
Buffer for 'D02:1' was adjusted by 3.31 SD.
Buffer for 'A06:1' was adjusted by 0.66 SD.
Buffer for 'E09:1' was adjusted by 0.09 SD.
Buffer for 'B01:1' was adjusted by 1.78 SD.
Buffer for 'A04:1' was adjusted by 1.53 SD.
Buffer for 'B06:1' was adjusted by 1.31 SD.
Buffer for 'F07:1' was adjusted by 0.13 SD.
Buffer for 'G08:1' was adjusted by 0.97 SD.
Buffer for 'E04:1' was adjusted by 1.22 SD.
Buffer for 'C02:1' was adjusted by 5.47 SD.
Buffer for 'A02:1' was adjusted by 2.10 SD.
Buffer for 'C09:1' was adjusted by 0.48 SD.
Buffer for 'C04:1' was adjusted by 2.42 SD.
Buffer for 'E03:1' was adjusted by 2.30 SD.
Buffer for 'D03:1' was adjusted by 2.13 SD.
Buffer for 'F02:1' was adjusted by 2.00 SD.
Buffer for 'C03:1' was adjusted by 4.13 SD.
Buffer for 'G02:1' was adjusted by 1.82 SD.
Buffer for 'H09:1' was adjusted by 0.67 SD.
Buffer for 'C01:1' was adjusted by 6.03 SD.
Buffer for 'H10:1' was adjusted by 0.40 SD.
Buffer for 'F09:1' was adjusted by 0.35 SD.
Buffer for 'E05:1' was adjusted by 0.44 SD.
Buffer for 'H01:1' was adjusted by 2.24 SD.
Buffer for 'B05:1' was adjusted by 0.72 SD.
Buffer for 'B04:1' was adjusted by 1.78 SD.
Buffer for 'H07:1' was adjusted by 0.62 SD.
Buffer for 'E08:1' was adjusted by 0.59 SD.
Buffer for 'D09:1' was adjusted by 0.44 SD.
Buffer for 'A03:1' was adjusted by 1.51 SD.
Buffer for 'A07:1' was adjusted by 1.89 SD.
Buffer for 'D05:2' was adjusted by 1.72 SD.
Buffer for 'E02:2' was adjusted by 1.67 SD.
Buffer for 'G05:2' was adjusted by 0.74 SD.
Buffer for 'D08:2' was adjusted by 1.49 SD.
Buffer for 'B02:2' was adjusted by 1.46 SD.
Buffer for 'B10:2' was adjusted by 0.91 SD.
Buffer for 'C06:2' was adjusted by 1.91 SD.
Buffer for 'C05:2' was adjusted by 1.03 SD.
Buffer for 'D04:2' was adjusted by 1.28 SD.
Buffer for 'D07:2' was adjusted by 0.97 SD.
Buffer for 'E07:2' was adjusted by 1.98 SD.
Buffer for 'B08:2' was adjusted by 1.52 SD.
Buffer for 'D02:2' was adjusted by 2.65 SD.
Buffer for 'A06:2' was adjusted by 1.60 SD.
Buffer for 'B01:2' was adjusted by 2.60 SD.
Buffer for 'A04:2' was adjusted by 2.37 SD.
Buffer for 'B06:2' was adjusted by 1.96 SD.
Buffer for 'G08:2' was adjusted by 1.08 SD.
Buffer for 'E04:2' was adjusted by 1.99 SD.
Buffer for 'C02:2' was adjusted by 7.26 SD.
Buffer for 'A02:2' was adjusted by 1.52 SD.
Buffer for 'C09:2' was adjusted by 1.09 SD.
Buffer for 'C04:2' was adjusted by 2.62 SD.
Buffer for 'E03:2' was adjusted by 3.11 SD.
Buffer for 'D03:2' was adjusted by 2.29 SD.
Buffer for 'F02:2' was adjusted by 1.85 SD.
Buffer for 'C03:2' was adjusted by 5.86 SD.
Buffer for 'G02:2' was adjusted by 1.96 SD.
Buffer for 'C01:2' was adjusted by 8.08 SD.
Buffer for 'B11:2' was adjusted by 0.61 SD.
Buffer for 'E05:2' was adjusted by 1.69 SD.
Buffer for 'H01:2' was adjusted by 2.03 SD.
Buffer for 'B05:2' was adjusted by 1.11 SD.
Buffer for 'B04:2' was adjusted by 2.00 SD.
Buffer for 'H07:2' was adjusted by 1.34 SD.
Buffer for 'E08:2' was adjusted by 1.59 SD.
Buffer for 'D09:2' was adjusted by 0.77 SD.
Buffer for 'A03:2' was adjusted by 2.15 SD.
Buffer for 'A07:2' was adjusted by 2.59 SD.
outlier in F11: [1 1 1 0 1 1 1 1 1 1 1 1 1 1].
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [K, S0_y1, S1_y1, S0_y2, S1_y2, x_diff, x_start, ye_mag]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 18 seconds.

MCMC Results:
Kd: 6.89
95% HDI: [6.75, 7.03]

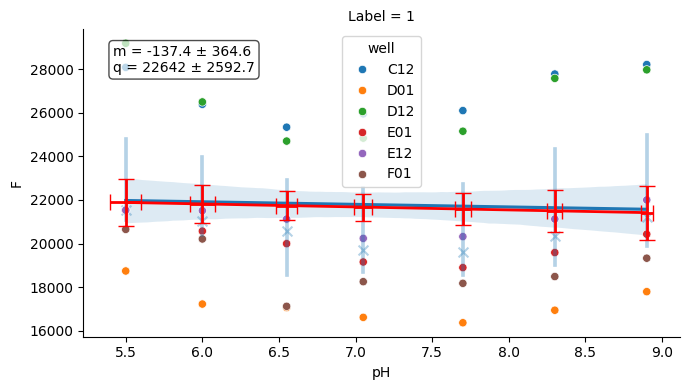
2.6. 6) Quality control and utilities

A few helper plots are useful to quickly assess experiment consistency (buffer, temperature).

# Buffer plot
buf_plot = tit.buffer.plot(nrm=False)
buf_plot.figure

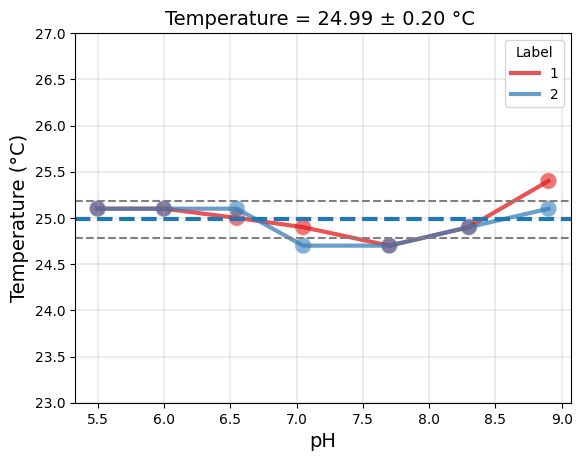
# Temperature plot
temp_plot = tit.plot_temperature()
temp_plot

import pandas as pd
import seaborn as sns

df1 = pd.read_csv(l2_dir / "fit1-1.csv", index_col=0)
# merged_df = tit.result_dfs[1][["K", "sK"]].merge(df1, left_index=True, right_index=True)
merged_df = tit.result_global.dataframe[["K", "sK"]].merge(
    df1, left_index=True, right_index=True
)

sns.jointplot(merged_df, x="K_y", y="K_x", ratio=3, space=0.4)

<seaborn.axisgrid.JointGrid at 0x7f7d6ca04ad0>

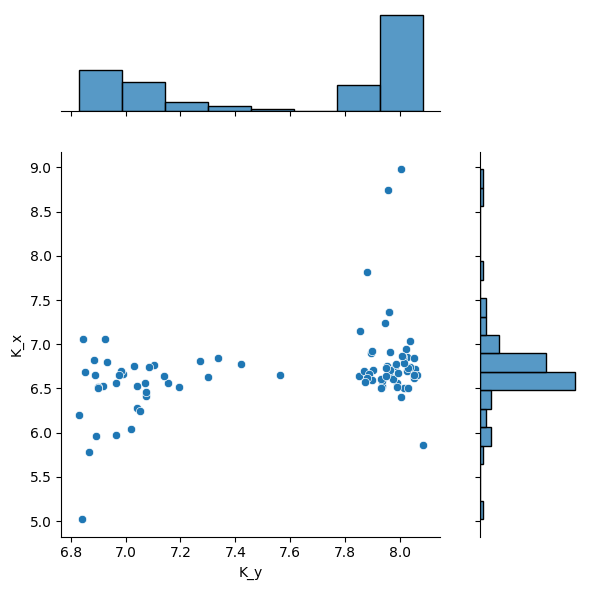
If a fit fails in a well, the well key will be anyway present in results list of dict.

tit.results[1].compute_all() conf = prtecan.TecanConfig(Path("jjj"), False, (), "", True, True) tit.export_data_fit(conf)

2.6.1. Posterior

from clophfit.fitting import plotting

np.random.seed(0)  # noqa: NPY002
remcee = glob.mini.emcee(
    burn=100,
    steps=2000,
    workers=8,
    thin=10,
    nwalkers=30,
    progress=False,
    is_weighted=True,
)

f = plotting.plot_emcee(remcee.flatchain)
print(remcee.flatchain.quantile([0.03, 0.97])["K"].to_list())

The chain is shorter than 50 times the integrated autocorrelation time for 5 parameter(s). Use this estimate with caution and run a longer chain!
N/50 = 40;
tau: [61.99995011 76.08980813 57.5356859  45.1407217  71.21607833]
[6.810901779453459, 6.936323228526876]

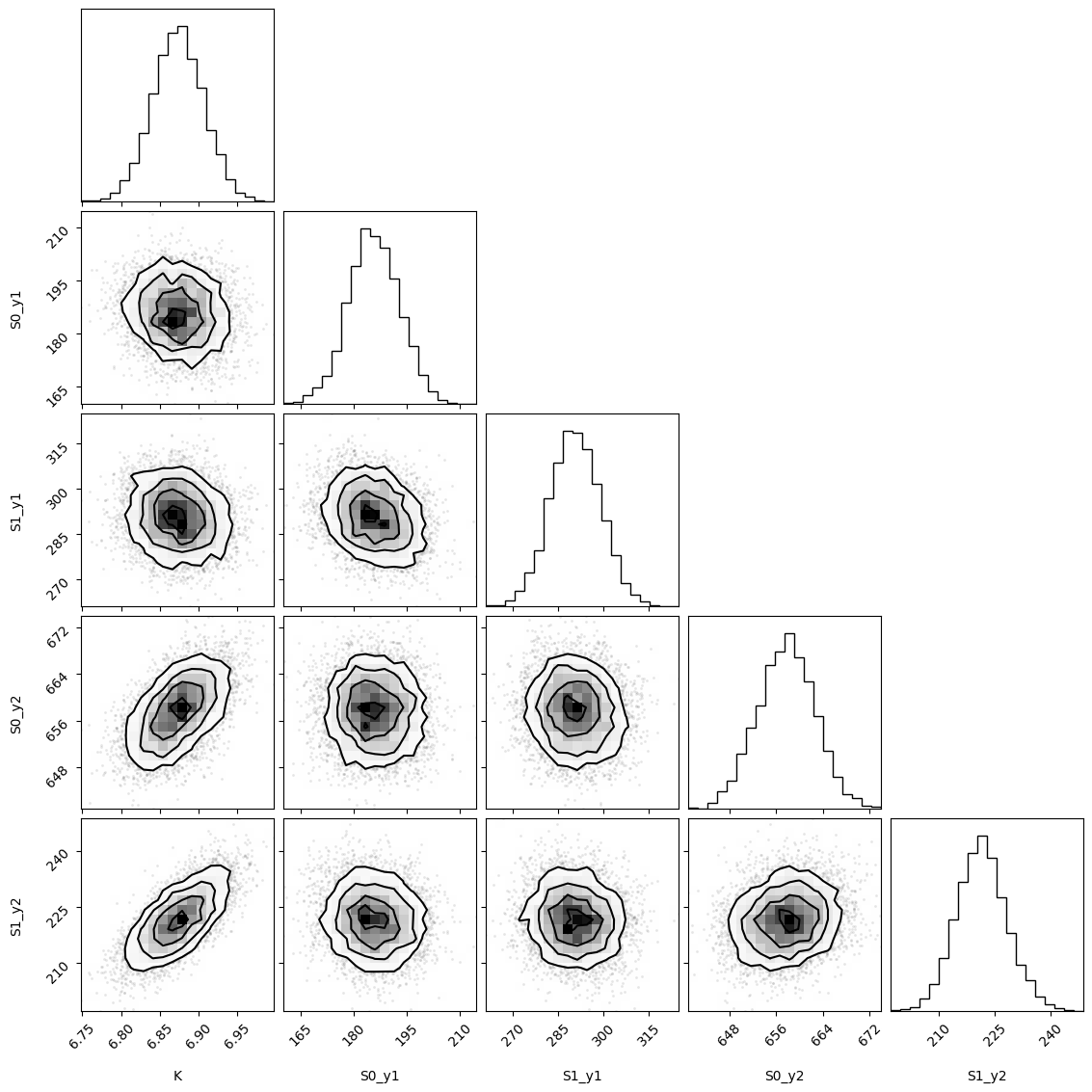
samples = remcee.flatchain[["K"]]
# Convert the dictionary of flatchains to an ArviZ InferenceData object
samples_dict = {key: np.array(val) for key, val in samples.items()}
idata = az.from_dict(posterior=samples_dict)
k_samples = idata.posterior["K"].to_numpy()
percentile_value = np.percentile(k_samples, 3)
print(f"Value at which the probability of being higher is 99%: {percentile_value}")

az.plot_forest(k_samples)

Value at which the probability of being higher is 99%: 6.810901779453459

array([<Axes: title={'center': '94.0% HDI'}>], dtype=object)

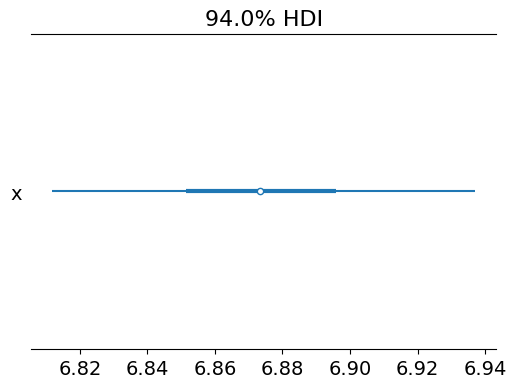
2.6.2. Combining

tit.result_global.compute_all()

with sns.axes_style("darkgrid"):
    g = sns.pairplot(
        tit.result_global.dataframe[["S1_y2", "S0_y2", "K", "S1_y1", "S0_y1"]],
        hue="S1_y1",
        palette="Reds",
        corner=True,
        diag_kind="kde",
    )

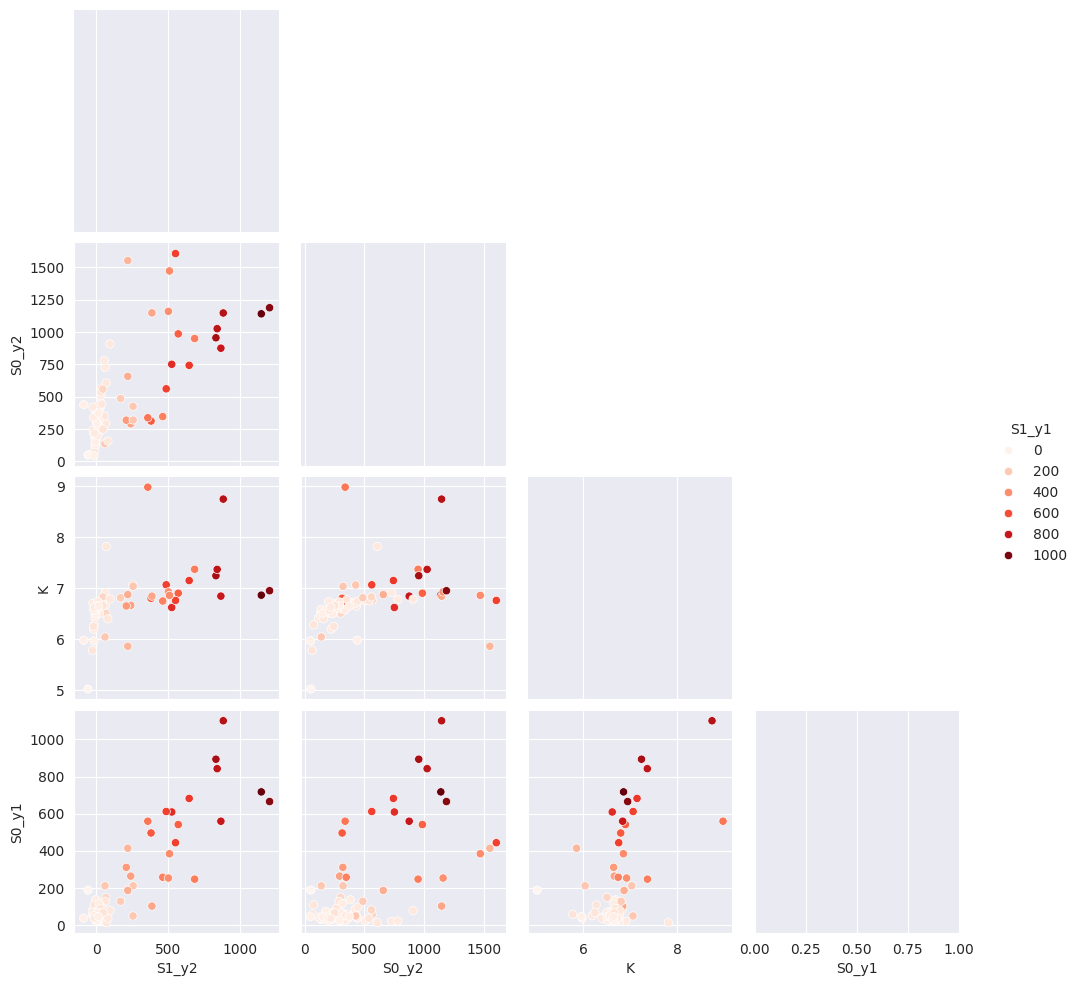
df_ctr = tit.results[1].dataframe
for name, wells in tit.scheme.names.items():
    for well in wells:
        df_ctr.loc[well, "ctrl"] = name

df_ctr.loc[df_ctr["ctrl"].isna(), "ctrl"] = "U"

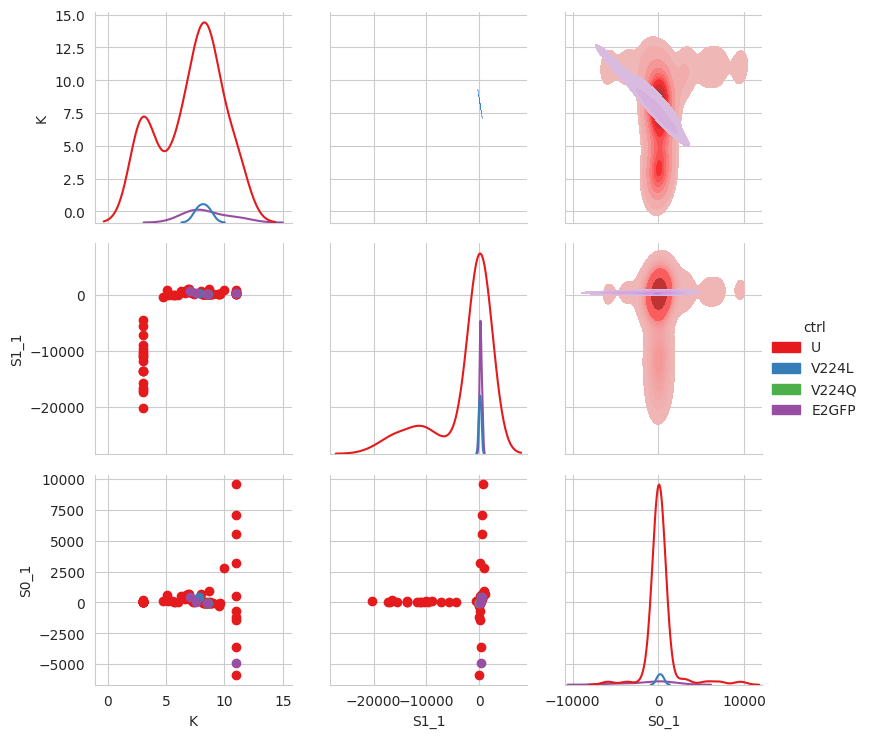
sns.set_style("whitegrid")
g = sns.PairGrid(
    df_ctr,
    x_vars=["K", "S1_1", "S0_1"],
    y_vars=["K", "S1_1", "S0_1"],
    hue="ctrl",
    palette="Set1",
    diag_sharey=False,
)
g.map_lower(plt.scatter)
g.map_upper(sns.kdeplot, fill=True)
g.map_diag(sns.kdeplot)
g.add_legend()

/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1615: UserWarning: KDE cannot be estimated (0 variance or perfect covariance). Pass `warn_singular=False` to disable this warning.
  func(x=x, y=y, **kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1615: UserWarning: KDE cannot be estimated (0 variance or perfect covariance). Pass `warn_singular=False` to disable this warning.
  func(x=x, y=y, **kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1615: UserWarning: KDE cannot be estimated (0 variance or perfect covariance). Pass `warn_singular=False` to disable this warning.
  func(x=x, y=y, **kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1615: UserWarning: KDE cannot be estimated (0 variance or perfect covariance). Pass `warn_singular=False` to disable this warning.
  func(x=x, y=y, **kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1615: UserWarning: KDE cannot be estimated (0 variance or perfect covariance). Pass `warn_singular=False` to disable this warning.
  func(x=x, y=y, **kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1513: UserWarning: Dataset has 0 variance; skipping density estimate. Pass `warn_singular=False` to disable this warning.
  func(x=vector, **plot_kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1513: UserWarning: Dataset has 0 variance; skipping density estimate. Pass `warn_singular=False` to disable this warning.
  func(x=vector, **plot_kwargs)
/home/runner/work/ClopHfit/ClopHfit/.venv/lib/python3.13/site-packages/seaborn/axisgrid.py:1513: UserWarning: Dataset has 0 variance; skipping density estimate. Pass `warn_singular=False` to disable this warning.
  func(x=vector, **plot_kwargs)

<seaborn.axisgrid.PairGrid at 0x7f7d53f71bd0>

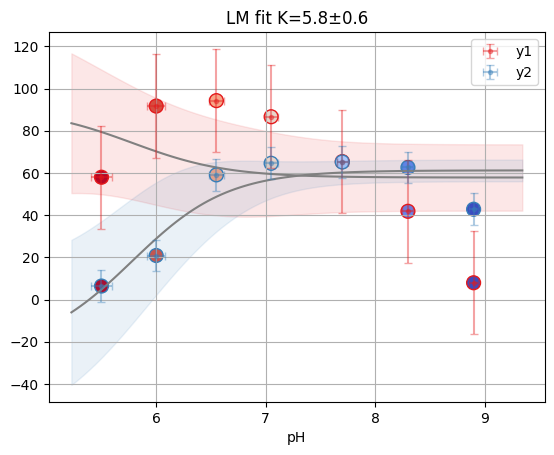
tit.result_global["A04"].figure

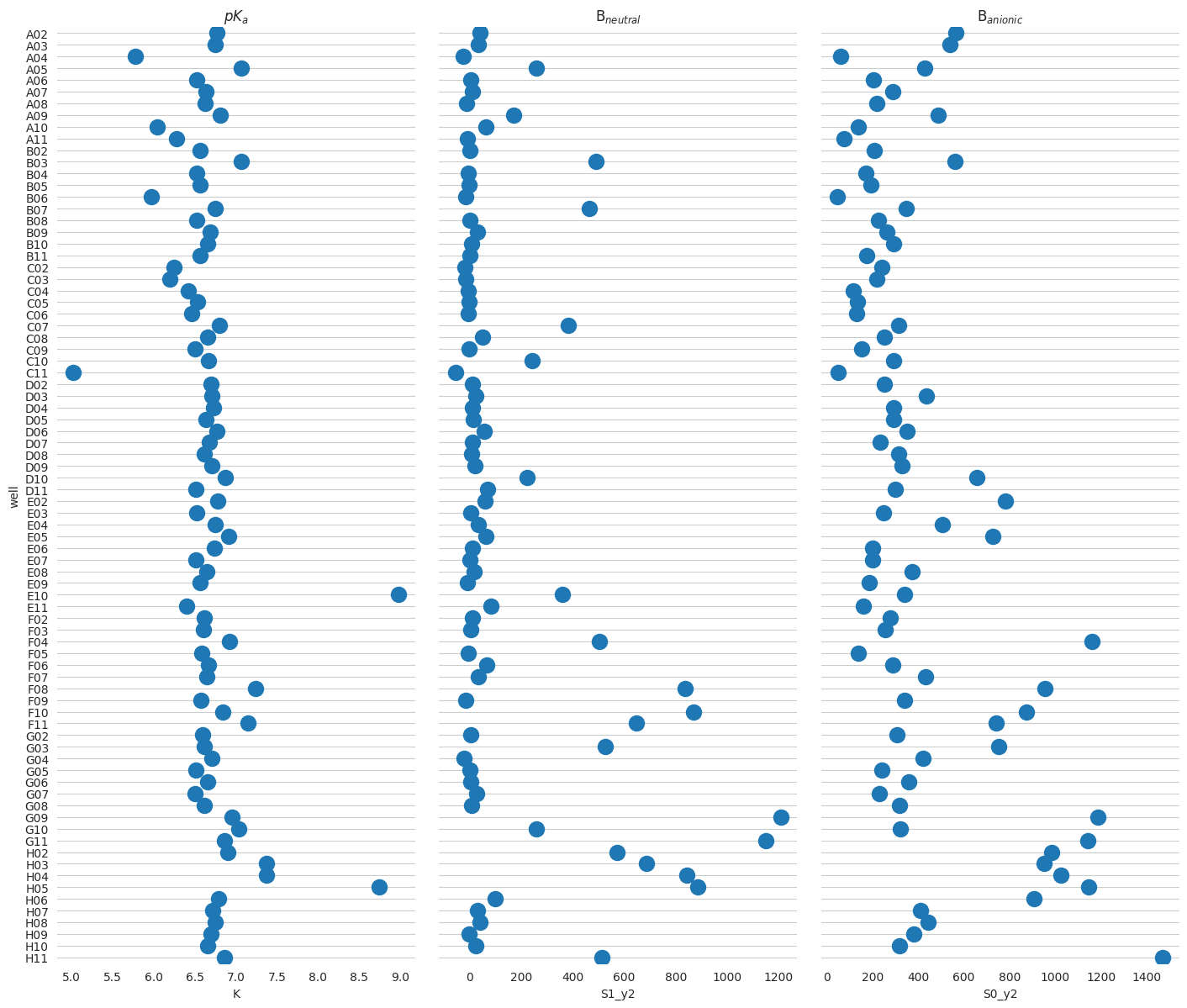
keys_unk = tit.fit_keys - set(tit.scheme.ctrl)
res_unk = tit.result_global.dataframe.loc[list(keys_unk)].sort_index()
res_unk["well"] = res_unk.index

f = plt.figure(figsize=(24, 14))
# Make the PairGrida
g = sns.PairGrid(
    res_unk,
    x_vars=["K", "S1_y2", "S0_y2"],
    y_vars="well",
    height=12,
    aspect=0.4,
)
# Draw a dot plot using the stripplot function
g.map(sns.stripplot, size=14, orient="h", palette="Set2", edgecolor="auto")

# Use the same x axis limits on all columns and add better labels
# g.set(xlim=(0, 25), xlabel="Crashes", ylabel="")

# Use semantically meaningful titles for the columns
titles = ["$pK_a$", "B$_{neutral}$", "B$_{anionic}$"]

for ax, title in zip(g.axes.flat, titles, strict=False):
    # Set a different title for each axes
    ax.set(title=title)

    # Make the grid horizontal instead of vertical
    ax.xaxis.grid(visible=False)
    ax.yaxis.grid(visible=True)

sns.despine(left=True, bottom=True)

<Figure size 2400x1400 with 0 Axes>

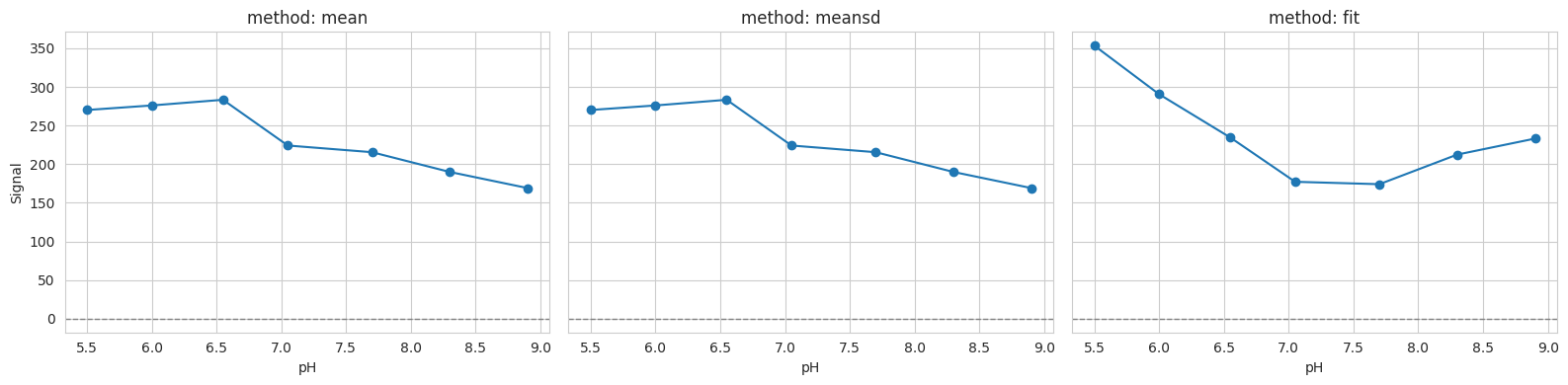
2.7. 7) Background method comparison

Different background methods may slightly shift baselines; inspect the impact on a single well.

methods = ["mean", "meansd", "fit"]
well = "D10"
fig, axes = plt.subplots(1, len(methods), figsize=(16, 4), sharey=True)
for ax, method in zip(axes, methods, strict=False):
    tit.params.bg_mth = method
    ax.plot(tit.x, tit.data[1][well], "o-", label=method)
    ax.axhline(0, color="gray", ls="--", lw=1)
    ax.set_title(f"method: {method}")
    ax.set_xlabel("pH")
axes[0].set_ylabel("Signal")
plt.tight_layout()

Buffer for 'D05:1' was adjusted by 0.72 SD.
Buffer for 'E02:1' was adjusted by 1.15 SD.
Buffer for 'F05:1' was adjusted by 0.50 SD.
Buffer for 'G05:1' was adjusted by 0.58 SD.
Buffer for 'D08:1' was adjusted by 0.54 SD.
Buffer for 'G04:1' was adjusted by 0.77 SD.
Buffer for 'B02:1' was adjusted by 1.24 SD.
Buffer for 'B10:1' was adjusted by 0.08 SD.
Buffer for 'C06:1' was adjusted by 1.34 SD.
Buffer for 'F03:1' was adjusted by 0.33 SD.
Buffer for 'C05:1' was adjusted by 0.91 SD.
Buffer for 'D04:1' was adjusted by 1.25 SD.
Buffer for 'D07:1' was adjusted by 0.52 SD.
Buffer for 'E07:1' was adjusted by 0.87 SD.
Buffer for 'B08:1' was adjusted by 0.79 SD.
Buffer for 'D02:1' was adjusted by 3.22 SD.
Buffer for 'A06:1' was adjusted by 0.64 SD.
Buffer for 'E09:1' was adjusted by 0.09 SD.
Buffer for 'B01:1' was adjusted by 1.73 SD.
Buffer for 'A04:1' was adjusted by 1.48 SD.
Buffer for 'B06:1' was adjusted by 1.27 SD.
Buffer for 'F07:1' was adjusted by 0.12 SD.
Buffer for 'G08:1' was adjusted by 0.95 SD.
Buffer for 'E04:1' was adjusted by 1.19 SD.
Buffer for 'C02:1' was adjusted by 5.32 SD.
Buffer for 'A02:1' was adjusted by 2.04 SD.
Buffer for 'C09:1' was adjusted by 0.47 SD.
Buffer for 'C04:1' was adjusted by 2.35 SD.
Buffer for 'E03:1' was adjusted by 2.24 SD.
Buffer for 'D03:1' was adjusted by 2.07 SD.
Buffer for 'F02:1' was adjusted by 1.95 SD.
Buffer for 'C03:1' was adjusted by 4.02 SD.
Buffer for 'G02:1' was adjusted by 1.76 SD.
Buffer for 'H09:1' was adjusted by 0.65 SD.
Buffer for 'C01:1' was adjusted by 5.86 SD.
Buffer for 'H10:1' was adjusted by 0.39 SD.
Buffer for 'F09:1' was adjusted by 0.35 SD.
Buffer for 'E05:1' was adjusted by 0.43 SD.
Buffer for 'H01:1' was adjusted by 2.18 SD.
Buffer for 'B05:1' was adjusted by 0.70 SD.
Buffer for 'B04:1' was adjusted by 1.73 SD.
Buffer for 'H07:1' was adjusted by 0.60 SD.
Buffer for 'E08:1' was adjusted by 0.57 SD.
Buffer for 'D09:1' was adjusted by 0.43 SD.
Buffer for 'A03:1' was adjusted by 1.46 SD.
Buffer for 'A07:1' was adjusted by 1.84 SD.
Buffer for 'D05:2' was adjusted by 1.64 SD.
Buffer for 'E02:2' was adjusted by 1.59 SD.
Buffer for 'G05:2' was adjusted by 0.70 SD.
Buffer for 'D08:2' was adjusted by 1.41 SD.
Buffer for 'B02:2' was adjusted by 1.39 SD.
Buffer for 'B10:2' was adjusted by 0.87 SD.
Buffer for 'C06:2' was adjusted by 1.82 SD.
Buffer for 'C05:2' was adjusted by 0.98 SD.
Buffer for 'D04:2' was adjusted by 1.22 SD.
Buffer for 'D07:2' was adjusted by 0.92 SD.
Buffer for 'E07:2' was adjusted by 1.88 SD.
Buffer for 'B08:2' was adjusted by 1.45 SD.
Buffer for 'D02:2' was adjusted by 2.52 SD.
Buffer for 'A06:2' was adjusted by 1.52 SD.
Buffer for 'B01:2' was adjusted by 2.48 SD.
Buffer for 'A04:2' was adjusted by 2.26 SD.
Buffer for 'B06:2' was adjusted by 1.86 SD.
Buffer for 'G08:2' was adjusted by 1.03 SD.
Buffer for 'E04:2' was adjusted by 1.89 SD.
Buffer for 'C02:2' was adjusted by 6.91 SD.
Buffer for 'A02:2' was adjusted by 1.45 SD.
Buffer for 'C09:2' was adjusted by 1.04 SD.
Buffer for 'C04:2' was adjusted by 2.50 SD.
Buffer for 'E03:2' was adjusted by 2.96 SD.
Buffer for 'D03:2' was adjusted by 2.18 SD.
Buffer for 'F02:2' was adjusted by 1.76 SD.
Buffer for 'C03:2' was adjusted by 5.58 SD.
Buffer for 'G02:2' was adjusted by 1.87 SD.
Buffer for 'C01:2' was adjusted by 7.69 SD.
Buffer for 'B11:2' was adjusted by 0.58 SD.
Buffer for 'E05:2' was adjusted by 1.61 SD.
Buffer for 'H01:2' was adjusted by 1.93 SD.
Buffer for 'B05:2' was adjusted by 1.05 SD.
Buffer for 'B04:2' was adjusted by 1.90 SD.
Buffer for 'H07:2' was adjusted by 1.28 SD.
Buffer for 'E08:2' was adjusted by 1.51 SD.
Buffer for 'D09:2' was adjusted by 0.73 SD.
Buffer for 'A03:2' was adjusted by 2.04 SD.
Buffer for 'A07:2' was adjusted by 2.47 SD.
Buffer for 'D05:1' was adjusted by 0.74 SD.
Buffer for 'E02:1' was adjusted by 1.18 SD.
Buffer for 'F05:1' was adjusted by 0.52 SD.
Buffer for 'G05:1' was adjusted by 0.60 SD.
Buffer for 'D08:1' was adjusted by 0.56 SD.
Buffer for 'G04:1' was adjusted by 0.79 SD.
Buffer for 'B02:1' was adjusted by 1.27 SD.
Buffer for 'B10:1' was adjusted by 0.08 SD.
Buffer for 'C06:1' was adjusted by 1.38 SD.
Buffer for 'F03:1' was adjusted by 0.33 SD.
Buffer for 'C05:1' was adjusted by 0.94 SD.
Buffer for 'D04:1' was adjusted by 1.29 SD.
Buffer for 'D07:1' was adjusted by 0.53 SD.
Buffer for 'E07:1' was adjusted by 0.89 SD.
Buffer for 'B08:1' was adjusted by 0.81 SD.
Buffer for 'D02:1' was adjusted by 3.31 SD.
Buffer for 'A06:1' was adjusted by 0.66 SD.
Buffer for 'E09:1' was adjusted by 0.09 SD.
Buffer for 'B01:1' was adjusted by 1.78 SD.
Buffer for 'A04:1' was adjusted by 1.53 SD.
Buffer for 'B06:1' was adjusted by 1.31 SD.
Buffer for 'F07:1' was adjusted by 0.13 SD.
Buffer for 'G08:1' was adjusted by 0.97 SD.
Buffer for 'E04:1' was adjusted by 1.22 SD.
Buffer for 'C02:1' was adjusted by 5.47 SD.
Buffer for 'A02:1' was adjusted by 2.10 SD.
Buffer for 'C09:1' was adjusted by 0.48 SD.
Buffer for 'C04:1' was adjusted by 2.42 SD.
Buffer for 'E03:1' was adjusted by 2.30 SD.
Buffer for 'D03:1' was adjusted by 2.13 SD.
Buffer for 'F02:1' was adjusted by 2.00 SD.
Buffer for 'C03:1' was adjusted by 4.13 SD.
Buffer for 'G02:1' was adjusted by 1.82 SD.
Buffer for 'H09:1' was adjusted by 0.67 SD.
Buffer for 'C01:1' was adjusted by 6.03 SD.
Buffer for 'H10:1' was adjusted by 0.40 SD.
Buffer for 'F09:1' was adjusted by 0.35 SD.
Buffer for 'E05:1' was adjusted by 0.44 SD.
Buffer for 'H01:1' was adjusted by 2.24 SD.
Buffer for 'B05:1' was adjusted by 0.72 SD.
Buffer for 'B04:1' was adjusted by 1.78 SD.
Buffer for 'H07:1' was adjusted by 0.62 SD.
Buffer for 'E08:1' was adjusted by 0.59 SD.
Buffer for 'D09:1' was adjusted by 0.44 SD.
Buffer for 'A03:1' was adjusted by 1.51 SD.
Buffer for 'A07:1' was adjusted by 1.89 SD.
Buffer for 'D05:2' was adjusted by 1.72 SD.
Buffer for 'E02:2' was adjusted by 1.67 SD.
Buffer for 'G05:2' was adjusted by 0.74 SD.
Buffer for 'D08:2' was adjusted by 1.49 SD.
Buffer for 'B02:2' was adjusted by 1.46 SD.
Buffer for 'B10:2' was adjusted by 0.91 SD.
Buffer for 'C06:2' was adjusted by 1.91 SD.
Buffer for 'C05:2' was adjusted by 1.03 SD.
Buffer for 'D04:2' was adjusted by 1.28 SD.
Buffer for 'D07:2' was adjusted by 0.97 SD.
Buffer for 'E07:2' was adjusted by 1.98 SD.
Buffer for 'B08:2' was adjusted by 1.52 SD.
Buffer for 'D02:2' was adjusted by 2.65 SD.
Buffer for 'A06:2' was adjusted by 1.60 SD.
Buffer for 'B01:2' was adjusted by 2.60 SD.
Buffer for 'A04:2' was adjusted by 2.37 SD.
Buffer for 'B06:2' was adjusted by 1.96 SD.
Buffer for 'G08:2' was adjusted by 1.08 SD.
Buffer for 'E04:2' was adjusted by 1.99 SD.
Buffer for 'C02:2' was adjusted by 7.26 SD.
Buffer for 'A02:2' was adjusted by 1.52 SD.
Buffer for 'C09:2' was adjusted by 1.09 SD.
Buffer for 'C04:2' was adjusted by 2.62 SD.
Buffer for 'E03:2' was adjusted by 3.11 SD.
Buffer for 'D03:2' was adjusted by 2.29 SD.
Buffer for 'F02:2' was adjusted by 1.85 SD.
Buffer for 'C03:2' was adjusted by 5.86 SD.
Buffer for 'G02:2' was adjusted by 1.96 SD.
Buffer for 'C01:2' was adjusted by 8.08 SD.
Buffer for 'B11:2' was adjusted by 0.61 SD.
Buffer for 'E05:2' was adjusted by 1.69 SD.
Buffer for 'H01:2' was adjusted by 2.03 SD.
Buffer for 'B05:2' was adjusted by 1.11 SD.
Buffer for 'B04:2' was adjusted by 2.00 SD.
Buffer for 'H07:2' was adjusted by 1.34 SD.
Buffer for 'E08:2' was adjusted by 1.59 SD.
Buffer for 'D09:2' was adjusted by 0.77 SD.
Buffer for 'A03:2' was adjusted by 2.15 SD.
Buffer for 'A07:2' was adjusted by 2.59 SD.
Buffer for 'A08:1' was adjusted by 0.33 SD.
Buffer for 'D05:1' was adjusted by 2.00 SD.
Buffer for 'E06:1' was adjusted by 0.50 SD.
Buffer for 'E02:1' was adjusted by 2.52 SD.
Buffer for 'F05:1' was adjusted by 1.60 SD.
Buffer for 'G05:1' was adjusted by 1.17 SD.
Buffer for 'D08:1' was adjusted by 1.58 SD.
Buffer for 'G04:1' was adjusted by 1.33 SD.
Buffer for 'B02:1' was adjusted by 1.87 SD.
Buffer for 'B10:1' was adjusted by 1.11 SD.
Buffer for 'C06:1' was adjusted by 2.58 SD.
Buffer for 'F03:1' was adjusted by 0.95 SD.
Buffer for 'E11:1' was adjusted by 0.44 SD.
Buffer for 'C05:1' was adjusted by 1.67 SD.
Buffer for 'D04:1' was adjusted by 2.38 SD.
Buffer for 'D07:1' was adjusted by 1.46 SD.
Buffer for 'E07:1' was adjusted by 1.97 SD.
Buffer for 'B08:1' was adjusted by 1.64 SD.
Buffer for 'D02:1' was adjusted by 4.81 SD.
Buffer for 'A06:1' was adjusted by 1.57 SD.
Buffer for 'E09:1' was adjusted by 0.63 SD.
Buffer for 'B01:1' was adjusted by 2.89 SD.
Buffer for 'A04:1' was adjusted by 2.52 SD.
Buffer for 'B06:1' was adjusted by 2.28 SD.
Buffer for 'F07:1' was adjusted by 0.47 SD.
Buffer for 'G08:1' was adjusted by 1.93 SD.
Buffer for 'E04:1' was adjusted by 2.65 SD.
Buffer for 'C02:1' was adjusted by 9.28 SD.
Buffer for 'A02:1' was adjusted by 3.03 SD.
Buffer for 'C09:1' was adjusted by 1.15 SD.
Buffer for 'C04:1' was adjusted by 4.29 SD.
Buffer for 'E03:1' was adjusted by 4.08 SD.
Buffer for 'D03:1' was adjusted by 3.41 SD.
Buffer for 'F02:1' was adjusted by 3.52 SD.
Buffer for 'C03:1' was adjusted by 7.29 SD.
Buffer for 'G02:1' was adjusted by 3.02 SD.
Buffer for 'H09:1' was adjusted by 0.29 SD.
Buffer for 'C01:1' was adjusted by 9.67 SD.
Buffer for 'H10:1' was adjusted by 0.61 SD.
Buffer for 'F09:1' was adjusted by 0.73 SD.
Buffer for 'E05:1' was adjusted by 1.16 SD.
Buffer for 'H01:1' was adjusted by 4.19 SD.
Buffer for 'B05:1' was adjusted by 1.58 SD.
Buffer for 'B04:1' was adjusted by 2.67 SD.
Buffer for 'H07:1' was adjusted by 1.74 SD.
Buffer for 'E08:1' was adjusted by 1.49 SD.
Buffer for 'D09:1' was adjusted by 1.29 SD.
Buffer for 'A03:1' was adjusted by 2.64 SD.
Buffer for 'A07:1' was adjusted by 3.32 SD.
Buffer for 'D05:2' was adjusted by 2.67 SD.
Buffer for 'E02:2' was adjusted by 2.57 SD.
Buffer for 'G05:2' was adjusted by 0.90 SD.
Buffer for 'D08:2' was adjusted by 2.25 SD.
Buffer for 'B02:2' was adjusted by 2.21 SD.
Buffer for 'B10:2' was adjusted by 1.22 SD.
Buffer for 'C06:2' was adjusted by 2.99 SD.
Buffer for 'C05:2' was adjusted by 1.42 SD.
Buffer for 'D04:2' was adjusted by 1.89 SD.
Buffer for 'D07:2' was adjusted by 1.32 SD.
Buffer for 'E07:2' was adjusted by 3.14 SD.
Buffer for 'B08:2' was adjusted by 2.31 SD.
Buffer for 'D02:2' was adjusted by 4.35 SD.
Buffer for 'A06:2' was adjusted by 2.46 SD.
Buffer for 'B01:2' was adjusted by 4.27 SD.
Buffer for 'A04:2' was adjusted by 3.79 SD.
Buffer for 'B06:2' was adjusted by 3.00 SD.
Buffer for 'G08:2' was adjusted by 1.52 SD.
Buffer for 'E04:2' was adjusted by 3.16 SD.
Buffer for 'C02:2' was adjusted by 12.65 SD.
Buffer for 'A02:2' was adjusted by 2.32 SD.
Buffer for 'C09:2' was adjusted by 1.53 SD.
Buffer for 'C04:2' was adjusted by 4.27 SD.
Buffer for 'E03:2' was adjusted by 5.18 SD.
Buffer for 'D03:2' was adjusted by 3.69 SD.
Buffer for 'F02:2' was adjusted by 2.91 SD.
Buffer for 'C03:2' was adjusted by 10.13 SD.
Buffer for 'G02:2' was adjusted by 3.11 SD.
Buffer for 'C01:2' was adjusted by 14.15 SD.
Buffer for 'B11:2' was adjusted by 0.67 SD.
Buffer for 'E05:2' was adjusted by 2.61 SD.
Buffer for 'H01:2' was adjusted by 3.23 SD.
Buffer for 'B05:2' was adjusted by 1.57 SD.
Buffer for 'B04:2' was adjusted by 3.15 SD.
Buffer for 'H07:2' was adjusted by 1.99 SD.
Buffer for 'E08:2' was adjusted by 2.44 SD.
Buffer for 'A03:2' was adjusted by 3.44 SD.
Buffer for 'A07:2' was adjusted by 4.25 SD.

You can decide how to pre-process data with datafit_params:

• [bg] subtract background

• [dil] apply correction for dilution (when e.g. during a titration you add titrant without protein)

• [nrm] normalize for gain, number of flashes and integration time.

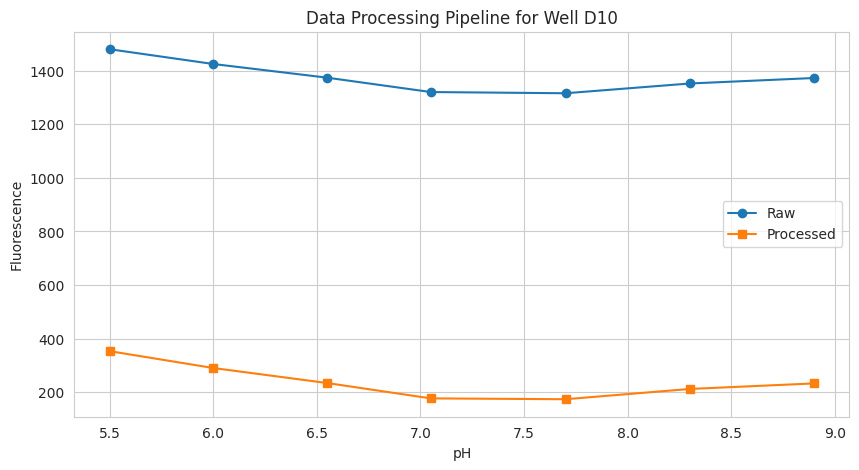
# 3.1 Accessing processed data
well = "D10"
data = {
    "pH": tit.x,
    "Signal (raw)": tit.labelblocksgroups[1].data_nrm[well],
    "Signal (processed)": tit.data[1][well],
}

plt.figure(figsize=(10, 5))
plt.plot(data["pH"], data["Signal (raw)"], "o-", label="Raw")
plt.plot(data["pH"], data["Signal (processed)"], "s-", label="Processed")
plt.xlabel("pH")
plt.ylabel("Fluorescence")
plt.title(f"Data Processing Pipeline for Well {well}")
plt.legend()
plt.grid(visible=True)

2.8. Cl titration analysis

cl_an = prtecan.Titration.fromlistfile(l2_dir / "list.cl.csv", is_ph=False)
cl_an.load_scheme(l2_dir / "scheme.txt")
cl_an.scheme

 OVER value in Label1: H02 of tecanfile ../../tests/Tecan/140220/pH5.0_200214.xls

PlateScheme(file=PosixPath('../../tests/Tecan/140220/scheme.txt'), _buffer=['D01', 'E01', 'D12', 'E12'], _discard=[], _ctrl=['A01', 'C12', 'H12', 'B12', 'H01', 'A12', 'F01', 'G01', 'F12', 'B01', 'G12', 'C01'], _names={'G03': {'A01', 'H12', 'B12'}, 'NTT': {'F01', 'C12', 'F12'}, 'S202N': {'H01', 'C01', 'G12'}, 'V224Q': {'G01', 'B01', 'A12'}})

from clophfit import prtecan

cl_an.load_additions(l2_dir / "additions.cl")
print(cl_an.x)
cl_an.x = prtecan.calculate_conc(cl_an.additions, 1000)
cl_an.x

[0. 0. 0. 0. 0. 0. 0. 0. 0.]

array([  0.        ,  17.54385965,  34.48275862,  50.84745763,
        66.66666667,  81.96721311,  96.77419355, 138.46153846,
       164.17910448])

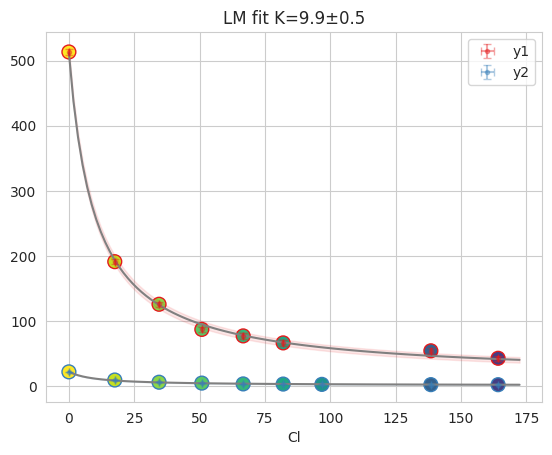
fres = cl_an.result_global["D10"]
print(fres.is_valid(), fres.result.bic, fres.result.redchi)
fres.figure

outlier in D10: [1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1].

True 12.838918069238009 1.3102777354816706

2.9. 8) Batch export (optional)

You can export processed data and fit results using TecanConfig. Note: adjust paths and toggles (png, fit, comb) as needed.

tit.params

TitrationConfig(bg=True, bg_adj=True, dil=True, nrm=True, bg_mth='fit', mcmc='single')

tit.params.bg_mth = "meansd"
tit.params.mcmc = None
tit.result_global.compute_all()

Buffer for 'D05:1' was adjusted by 0.74 SD.
Buffer for 'E02:1' was adjusted by 1.18 SD.
Buffer for 'F05:1' was adjusted by 0.52 SD.
Buffer for 'G05:1' was adjusted by 0.60 SD.
Buffer for 'D08:1' was adjusted by 0.56 SD.
Buffer for 'G04:1' was adjusted by 0.79 SD.
Buffer for 'B02:1' was adjusted by 1.27 SD.
Buffer for 'B10:1' was adjusted by 0.08 SD.
Buffer for 'C06:1' was adjusted by 1.38 SD.
Buffer for 'F03:1' was adjusted by 0.33 SD.
Buffer for 'C05:1' was adjusted by 0.94 SD.
Buffer for 'D04:1' was adjusted by 1.29 SD.
Buffer for 'D07:1' was adjusted by 0.53 SD.
Buffer for 'E07:1' was adjusted by 0.89 SD.
Buffer for 'B08:1' was adjusted by 0.81 SD.
Buffer for 'D02:1' was adjusted by 3.31 SD.
Buffer for 'A06:1' was adjusted by 0.66 SD.
Buffer for 'E09:1' was adjusted by 0.09 SD.
Buffer for 'B01:1' was adjusted by 1.78 SD.
Buffer for 'A04:1' was adjusted by 1.53 SD.
Buffer for 'B06:1' was adjusted by 1.31 SD.
Buffer for 'F07:1' was adjusted by 0.13 SD.
Buffer for 'G08:1' was adjusted by 0.97 SD.
Buffer for 'E04:1' was adjusted by 1.22 SD.
Buffer for 'C02:1' was adjusted by 5.47 SD.
Buffer for 'A02:1' was adjusted by 2.10 SD.
Buffer for 'C09:1' was adjusted by 0.48 SD.
Buffer for 'C04:1' was adjusted by 2.42 SD.
Buffer for 'E03:1' was adjusted by 2.30 SD.
Buffer for 'D03:1' was adjusted by 2.13 SD.
Buffer for 'F02:1' was adjusted by 2.00 SD.
Buffer for 'C03:1' was adjusted by 4.13 SD.
Buffer for 'G02:1' was adjusted by 1.82 SD.
Buffer for 'H09:1' was adjusted by 0.67 SD.
Buffer for 'C01:1' was adjusted by 6.03 SD.
Buffer for 'H10:1' was adjusted by 0.40 SD.
Buffer for 'F09:1' was adjusted by 0.35 SD.
Buffer for 'E05:1' was adjusted by 0.44 SD.
Buffer for 'H01:1' was adjusted by 2.24 SD.
Buffer for 'B05:1' was adjusted by 0.72 SD.
Buffer for 'B04:1' was adjusted by 1.78 SD.
Buffer for 'H07:1' was adjusted by 0.62 SD.
Buffer for 'E08:1' was adjusted by 0.59 SD.
Buffer for 'D09:1' was adjusted by 0.44 SD.
Buffer for 'A03:1' was adjusted by 1.51 SD.
Buffer for 'A07:1' was adjusted by 1.89 SD.
Buffer for 'D05:2' was adjusted by 1.72 SD.
Buffer for 'E02:2' was adjusted by 1.67 SD.
Buffer for 'G05:2' was adjusted by 0.74 SD.
Buffer for 'D08:2' was adjusted by 1.49 SD.
Buffer for 'B02:2' was adjusted by 1.46 SD.
Buffer for 'B10:2' was adjusted by 0.91 SD.
Buffer for 'C06:2' was adjusted by 1.91 SD.
Buffer for 'C05:2' was adjusted by 1.03 SD.
Buffer for 'D04:2' was adjusted by 1.28 SD.
Buffer for 'D07:2' was adjusted by 0.97 SD.
Buffer for 'E07:2' was adjusted by 1.98 SD.
Buffer for 'B08:2' was adjusted by 1.52 SD.
Buffer for 'D02:2' was adjusted by 2.65 SD.
Buffer for 'A06:2' was adjusted by 1.60 SD.
Buffer for 'B01:2' was adjusted by 2.60 SD.
Buffer for 'A04:2' was adjusted by 2.37 SD.
Buffer for 'B06:2' was adjusted by 1.96 SD.
Buffer for 'G08:2' was adjusted by 1.08 SD.
Buffer for 'E04:2' was adjusted by 1.99 SD.
Buffer for 'C02:2' was adjusted by 7.26 SD.
Buffer for 'A02:2' was adjusted by 1.52 SD.
Buffer for 'C09:2' was adjusted by 1.09 SD.
Buffer for 'C04:2' was adjusted by 2.62 SD.
Buffer for 'E03:2' was adjusted by 3.11 SD.
Buffer for 'D03:2' was adjusted by 2.29 SD.
Buffer for 'F02:2' was adjusted by 1.85 SD.
Buffer for 'C03:2' was adjusted by 5.86 SD.
Buffer for 'G02:2' was adjusted by 1.96 SD.
Buffer for 'C01:2' was adjusted by 8.08 SD.
Buffer for 'B11:2' was adjusted by 0.61 SD.
Buffer for 'E05:2' was adjusted by 1.69 SD.
Buffer for 'H01:2' was adjusted by 2.03 SD.
Buffer for 'B05:2' was adjusted by 1.11 SD.
Buffer for 'B04:2' was adjusted by 2.00 SD.
Buffer for 'H07:2' was adjusted by 1.34 SD.
Buffer for 'E08:2' was adjusted by 1.59 SD.
Buffer for 'D09:2' was adjusted by 0.77 SD.
Buffer for 'A03:2' was adjusted by 2.15 SD.
Buffer for 'A07:2' was adjusted by 2.59 SD.
outlier in F11: [1 1 1 0 1 1 1 1 1 1 1 1 1 1].

tit.results[1].compute_all()
tit.results[2].compute_all()

tit.result_odr.compute_all()

from tempfile import mkdtemp

out_dir = Path(mkdtemp())
conf = prtecan.TecanConfig(
    out_fp=out_dir, comb=False, lim=None, title="FullAnalysis", fit=True, png=True
)
tit.export_data_fit(conf)
print("Exported to:", out_dir)
# list(out_dir.glob('*'))[:10]
# print("Contents:", *[f.name for f in output_dir.glob("*")], sep="\n- ")

Exported to: /tmp/tmpvgczkfib